Colles de mathématiques
"Astroïde" trigonométrique
Sujet
Étudier et tracer la courbe C d'équations paramétriques
x(t)
=
cos3t
y(t)
=
sin3t
Corrigé de l'exercice de maths: Courbes paramétrées
Correction
Les fonctions 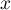 et
et  sont
sont  -périodiques,
on peut donc restreindre le domaine d'étude à
-périodiques,
on peut donc restreindre le domaine d'étude à ![$[-\pi,\pi]$](/Generateur-Devoirs/Colles/courbesparam/ex2_c/4.png) .
On remarque ensuite que
.
On remarque ensuite que  et
et 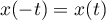 .
On peut donc restreindre le domaine d'étude à
.
On peut donc restreindre le domaine d'étude à ![$[0,\pi]$](/Generateur-Devoirs/Colles/courbesparam/ex2_c/7.png) , on déduira le
reste de la courbe par une symétrie d'axe
, on déduira le
reste de la courbe par une symétrie d'axe 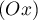 .
De plus
.
De plus  et
et 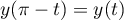 .
On peut à nouveau réduire l'intervalle d'étude à
.
On peut à nouveau réduire l'intervalle d'étude à ![$[0,\pi/2]$](/Generateur-Devoirs/Colles/courbesparam/ex2_c/11.png) ,
puis faire une symétrie d'axe
,
puis faire une symétrie d'axe 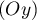 .
Enfin, on a
.
Enfin, on a 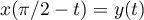 et
et  . On peut donc encore réduire l'intervalle d'étude à
. On peut donc encore réduire l'intervalle d'étude à ![$[0,\pi/4]$](/Generateur-Devoirs/Colles/courbesparam/ex2_c/15.png) , puis faire une symétrie par rapport
à la première bissectrice du repère.
, puis faire une symétrie par rapport
à la première bissectrice du repère.
Étudions maintenant les fonctions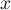 et
et  sur l'intervalle
sur l'intervalle ![$[0,\pi/4]$](/Generateur-Devoirs/Colles/courbesparam/ex2_c/18.png) .
Elles y sont dérivables, de dérivée
.
Elles y sont dérivables, de dérivée
![\[x'(t)=-3\cos^2 t \sin t\textrm{ et }y'(t)=3\sin^2 t \cos t.\]](/Generateur-Devoirs/Colles/courbesparam/ex2_c/19.png)
Ceci permet de dresser le tableau suivant :

Le point correspondant à , de coordonnée
, de coordonnée  ,
est donc un point stationnaire.
,
est donc un point stationnaire.
On détermine la tangente en ce point en étudiant la limite de lorsque
lorsque  tend vers 0:
tend vers 0:
![\[\frac{y'(t)}{x'(t)}=\tan t\to 0.\]](/Generateur-Devoirs/Colles/courbesparam/ex2_c/25.png)
En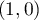 , la courbe admet donc une tangente horizontale.
On peut vérifier à l'aide de développements limités que
, la courbe admet donc une tangente horizontale.
On peut vérifier à l'aide de développements limités que 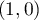 est
un point de rebroussement de première espèce pour la courbe.
est
un point de rebroussement de première espèce pour la courbe.
On obtient finalement le tracé suivant :

Étudions maintenant les fonctions
Ceci permet de dresser le tableau suivant :

Le point correspondant à
On détermine la tangente en ce point en étudiant la limite de
En
On obtient finalement le tracé suivant :
