Colles de mathématiques
Alignement de z, z2 et z4
Sujet
Déterminer 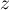 tel que les points d'affixe
tel que les points d'affixe 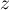 ,
, 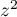 et
et 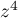 soient alignés.
soient alignés.
Corrigé de l'exercice de maths: Nombres complexes
Correction
Les points 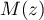 ,
, 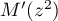 et
et 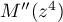 sont alignés
si et seulement si il existe
sont alignés
si et seulement si il existe  tel que
tel que
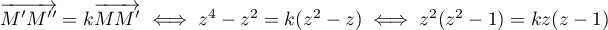 .
.
Les points sont alignés pour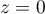 et
et  (tous les points sont confondus)
et, si
(tous les points sont confondus)
et, si 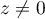 et
et  ,
,
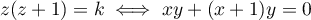 soit pour
soit pour 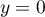 (axe des abscisses)
ou si
(axe des abscisses)
ou si 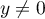 ,
,  .
.
Les points sont alignés pour