Colles de mathématiques
Calcul d'intégrale avec changement de variable
Sujet
Calculer 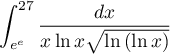 en posant
en posant 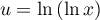 .
.
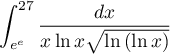 en posant
en posant Corrigé de l'exercice de maths: Intégrales sur un segment
Correction
Soit 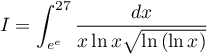 et le changement de variable
et le changement de variable 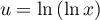 ,
alors
,
alors 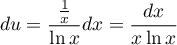 et alors,
et alors,
![I=\int_1^{\ln(3\ln 3)} \dfrac{du}{\sqrt{u}}=2[\sqrt{u}]_1^{\ln\lp3\ln 3\right)}=2(\sqrt{\ln(3\ln 3)}-1)](/Generateur-Devoirs/Colles/Integrale/exCchgt4_c/4.png)
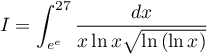 et le changement de variable
et le changement de variable ![I=\int_1^{\ln(3\ln 3)} \dfrac{du}{\sqrt{u}}=2[\sqrt{u}]_1^{\ln\lp3\ln 3\right)}=2(\sqrt{\ln(3\ln 3)}-1)](/Generateur-Devoirs/Colles/Integrale/exCchgt4_c/4.png)