🔍

Colles de mathématiques

Calculer l'intégrale …


Sujet


Calculer ∫ −∞ +∞ x2e−x2 dx sachant que ∫ −∞ +∞ e−x2 dx = π

Corrigé de l'exercice de maths: Intégrales généralisées

Correction


En intégrant par parties, pour faire apparaître l'intégrale donnée dans l'énoncé,
\int_{-\infty}^{+\infty}x^2e^{-x^2}\,dx=\int_{-\infty}^{+\infty}x ( xe^{-x^2})dx=[x\dfrac{e^{-x^2}}{-2}]_{-\infty}^{+\infty}-\int_{-\infty}^{+\infty}\dfrac{e^{-x^2}}{-2}\,dx=\dfrac12\sqrt\pi

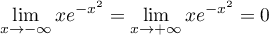car, par croissances comparées, $\dsp\lim_{x\to-\infty}xe^{-x^2}=\lim_{x\to+\infty}xe^{-x^2}=0$.