🔍

Colles de mathématiques

Étude de la convergence de la série


Sujet


Déterminer la nature de la série de terme général un = 1n − 1n + 1 − 1nn

Corrigé de l'exercice de maths: Séries

Correction


On a
\[\begin{array}{ll}\dfrac1{\sqrt{n+1}} &=\dfrac1{\sqrt{n}\sqrt{1+\frac1n}}\\[1.2em] &=\dfrac1{\sqrt{n}}\lp1+\dfrac1n\rp^{-1/2}\\[1.2em] &=\dfrac1{\sqrt{n}}\lp1-\dfrac1{2n}+o\lp\dfrac1n\rp\rp \enar\]

et
\[\begin{array}{ll}u_n&=\dfrac{1}{\sqrt{n}}-\dfrac{1}{\sqrt{n+1}}-\dfrac{1}{n\sqrt{n}}\\ &=-\dfrac1{2n\sqrt{n}}+o\lp\dfrac1{n\sqrt{n}}\rp\enar\]

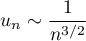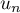Ainsi, $u_n\sim\dfrac1{n^{3/2}}$ et donc, par comparaison avec les séries de Riemann, comme $3/2>1$, on en déduit que la série de terme général $u_n$ est convergente.