Colles de mathématiques
Intégrale trigonométrique
Sujet
Calculer l'intégrale
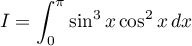
Corrigé de l'exercice de maths: Intégrales sur un segment
Correction
On peut procéder suivant (au moins) deux méthodes.
Formule d'Euler.
On peut commencer par écrire
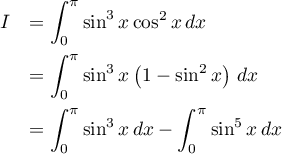
puis, avec la formule d'Euler et la formule du binôme de Newton:
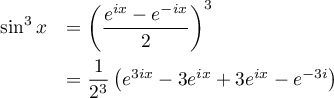
puis, en regroupant les termes, et à nouveau la formule d'Euler,
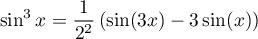
De même,
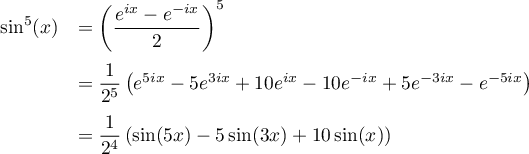
On a alors,
![I=\int_0^\pi\sin^3x dx-\int_0^\pi\sin^5x dx=\dfrac1{2^2}[-\dfrac{\cos(3x)}3+3\cos(x)]_0^\pi -\dfrac1{2^4}[-\dfrac{\cos(5x)}{5}+5\dfrac{\cos(3x)}3-10\cos(x)]_0^\pi =\dfrac4{15}](/Generateur-Devoirs/Colles/Integrale/exCchgt5_c/5.png)
Changement de variable.
Comme la fonction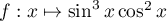 est impaire,
il est judicieux d'effectuer le changement de variable
est impaire,
il est judicieux d'effectuer le changement de variable
 .
.
On a alors,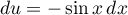 et
et
![I=\int_0^\pi \cos^2 x \sin^2x\sin x dx=-\int_1^{-1} u^2(1-u^2)du=\int_{-1}^1u^2\,du-\int_{-1}^1u^4 du =2\int_0^1u^2 du-2\int_0^1u^4 du = 2[\dfrac{u^3}3]_0^1-2[\dfrac{u^5}5]_0^1=\dfrac23-\dfrac25=\dfrac4{15}](/Generateur-Devoirs/Colles/Integrale/exCchgt5_c/9.png)
Formule d'Euler.
On peut commencer par écrire
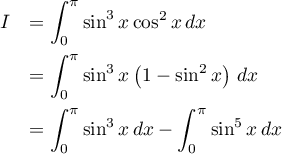
puis, avec la formule d'Euler et la formule du binôme de Newton:
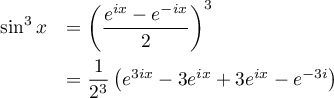
puis, en regroupant les termes, et à nouveau la formule d'Euler,
De même,
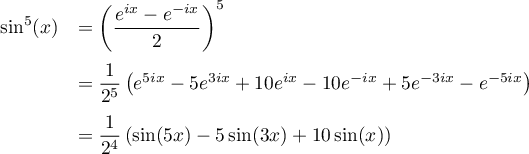
On a alors,
![I=\int_0^\pi\sin^3x dx-\int_0^\pi\sin^5x dx=\dfrac1{2^2}[-\dfrac{\cos(3x)}3+3\cos(x)]_0^\pi -\dfrac1{2^4}[-\dfrac{\cos(5x)}{5}+5\dfrac{\cos(3x)}3-10\cos(x)]_0^\pi =\dfrac4{15}](/Generateur-Devoirs/Colles/Integrale/exCchgt5_c/5.png)
Changement de variable.
Comme la fonction
On a alors,
![I=\int_0^\pi \cos^2 x \sin^2x\sin x dx=-\int_1^{-1} u^2(1-u^2)du=\int_{-1}^1u^2\,du-\int_{-1}^1u^4 du =2\int_0^1u^2 du-2\int_0^1u^4 du = 2[\dfrac{u^3}3]_0^1-2[\dfrac{u^5}5]_0^1=\dfrac23-\dfrac25=\dfrac4{15}](/Generateur-Devoirs/Colles/Integrale/exCchgt5_c/9.png)