Colles de mathématiques
Intégrales trigonométriques et famille de fonctions trigonométriques libre
Exercice de maths: Intégrales sur un segment - Espaces vectoriels
Sujet
- Pour
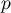 et
et 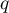 des entiers naturels donnés, calculer
les intégrales
des entiers naturels donnés, calculer
les intégrales
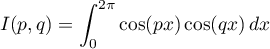 ,
,
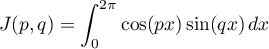 , et
, et
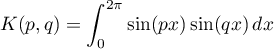 .
.
- Montrer que la famille de fonctions
 est libre.
est libre.