Colles de mathématiques
Séries à partir d'une suite implicite
Oral ESCP - filière B/L, 2021
Exercice de maths: Séries - Annales ESCP - B/L
Sujet
Oral ESCP, BL - 2021
- Soit
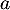 un réel positif ou nul. Pour tout
un réel positif ou nul. Pour tout 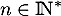 , on considère l'équation d'inconnue
, on considère l'équation d'inconnue 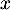 réel
réel
![\[x^n+n^ax-1=0\]](/Generateur-Devoirs/Colles/Series/ESCP-BL-2021-4.2/4.png)
Montrer que cette équation admet une seule solution sur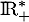 .
On la note
.
On la note 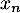 .
.
- Étudier la convergence de la suite
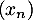 .
.
- On suppose
 .
.
- Montrer que
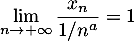
- Soit
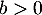 . Étudier la convergence des séries suivantes:
. Étudier la convergence des séries suivantes:
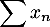 ,
,
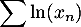 ,
,
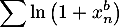 , et
, et
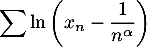
- Montrer que