🔍

Colles de mathématiques

Suite definie par une integrale généralisée

Oral ENS Ulm, filière B/L, 2021



Exercice de maths: Intégrales généralisées - Suites - Annales ENS Ulm - B/L

Sujet


On définit la suite 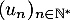$(u_n)_{n\in\mathbb{ N}^*}$ par :
\[u_n=\dsp\int_0^{+\infty} \dfrac{e^{-x}}{x+\frac{1}{n}} dx\]

  1. Justifier que la suite $(u_n)_{n\in \mathbb{ N}^*}$ est bien définie et étudier son sens de variation.
  2. On définit, pour tout $n\in\N^*$,
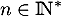    \[v_n=\dsp\int_0^{1} \dfrac{e^{-x}}{x+\frac{1}{n}} dx \quad \text{ et }\quad w_n=\displaystyle\int_1^{+\infty} \dfrac{e^{-x}}{x+\frac{1}{n}} dx \]

    Montrer que, pour tout $n\in\N^*$ :
    \[v_n\geq \dfrac{\ln(n+1)}{e}\quad\text{ et }\quad 0\leq w_n\leq \dfrac{1}{e}\]


  3. Donner la limite de la suite $(u_n)$.
  4. On cherche maintenant à obtenir un résultat plus précis.
    1. Montre que l'intégrale 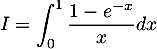$I=\dsp\int_0^1 \dfrac{1-e^{-x}}{x} dx$ est convergente.
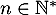    2. Montrer que pour tout $n\in\mathbb{N}^*$ :
      \[0\leq \dsp\int_0^{1} \dfrac{1-e^{-x}}{x+\frac{1}{n}} dx \leq I\]

    3. En déduire que :
      \[\lim\limits_{\substack{n \rightarrow +\infty }} \dfrac{u_n}{\ln(n)}=1\]

Correction