Colles de mathématiques
Suite et série télescopique
Exercice de maths: Séries - Suites
Sujet
Soit 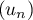 une suite de réels positifs décroissante et tendant vers 0.
Soit
une suite de réels positifs décroissante et tendant vers 0.
Soit 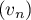 la suite définie par
la suite définie par
![\[v_n=\lp\sum_{k=1}^nu_k\rp-nu_n\]](/Generateur-Devoirs/Colles/Series/sst/3.png)
![\[v_n=\lp\sum_{k=1}^nu_k\rp-nu_n\]](/Generateur-Devoirs/Colles/Series/sst/3.png)
- On suppose dans cette question que la série de terme général
 converge.
Montrer que
converge.
Montrer que 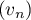 est bornée.
est bornée.
- On suppose dans cette question que la suite
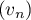 est bornée.
est bornée.
- Calculer
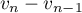
- Montrer que la suite
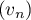 converge.
converge.
- Montrer que la série de terme général
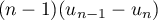 converge.
converge.
- Montrer que
![\[\sum_{k=n+1}^\infty(k-1)(u_{k-1}-u_k)\geqslant nu_n\]](/Generateur-Devoirs/Colles/Series/sst/10.png)
- Montrer que la série de terme général
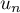 converge.
converge.
- Calculer