Colles de mathématiques
Calculer l'intégrale …
Sujet
Calculer l'intégrale
∫
0
π2
x sin3(x) dx
Corrigé de l'exercice de maths: Intégrales sur un segment
Correction
Avec la formule d'Euler pour linéariser le
sin3,
on a
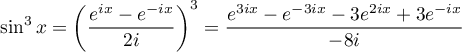
et on peut continuer les calculs avec les complexes, en utilisant
![\int_0^{\frac\pi2}xe^{\alpha x}\,dx=[\dfrac1\alpha xe^{\alpha x}]_0^{\frac\pi2}-\dfrac1\alpha\int_0^{\frac\pi2}e^{\alpha x}\,dx=\dfrac{\pi}{2\alpha}e^{\frac{\alpha\pi}{2}}-\dfrac{1}{\alpha^2}(e^{\frac{\alpha\pi}{2}}-1)](/Generateur-Devoirs/Colles/Integrale/exC5_c/3.png)
d'où, par linéarité et avec α = −i d'une part et α = i d'autre part, on obtient finalement
![\[\int_0^{\frac\pi2} x\sin^3 x\,dx=\dfrac79\]](/Generateur-Devoirs/Colles/Integrale/exC5_c/4.png)
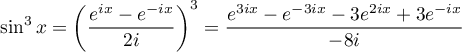
et on peut continuer les calculs avec les complexes, en utilisant
d'où, par linéarité et avec α = −i d'une part et α = i d'autre part, on obtient finalement