🔍

Colles de mathématiques

Calculer l'intégrale


Sujet


Calculer l'intégrale 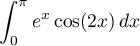$\int_0^\pi e^x\cos(2x)\,dx$

Corrigé de l'exercice de maths: Intégrales sur un segment

Correction


Soit 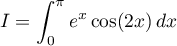$I=\dsp\int_0^\pi e^x\cos(2x)\,dx$.
On peut penser soit à une (deux en fait) intégration par parties, soit à utiliser les complexes.

IPP: On dérive par exemple l'exponentielle et intègre le cosinus:
I=\underbrace{[e^x\dfrac{\sin(2x)}2]_0^\pi}_{=0}-\int_0^\pi e^x\dfrac{\sin(2x)}2dx

puis, en intégrant une nouvelle fois par parties, en dérivant à nouveau l'exponentielle et intégrant le sinus,
I=[e^x\dfrac{\cos(2x)}4]_0^\pi-\int_0^\pi e^x\dfrac{\cos(2x)}4\,dx=\dfrac14(e^\pi-1\rp-\dfrac14 I

On en déduit que
I=\dfrac15(e^\pi-1)



Complexes: On a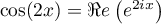 \cos(2x)=\Re e(e^{2ix}) et donc
I=\Re(\int_0^\pi e^xe^{2ix}dx)=\Re(\int_0^\pi e^{x(1+2i)}\,dx)\Re(\dfrac1{1+2i}[e^{x(1+2i)}]_0^\pi)=\Re(\dfrac{1-2i}5(e^{\pi(1+2i)}-1))

or e^{\pi(1+2i)}=e^\pi e^{2i\pi}=e^\pi et donc
I=\dfrac15((e^\pi-1)