Colles de mathématiques
Construction d'une base orthonormale directe
Sujet
Déterminer une base orthonormale directe de l'espace dont le premier vecteur est colinéaire au vecteur
(1; 2; 2).
Corrigé de l'exercice de maths: Géométrie dans l'espace
Correction
On trouve un vecteur orthogonal, par exemple
 , puis un 3ème vecteur grâce au produit vectoriel:
, puis un 3ème vecteur grâce au produit vectoriel:
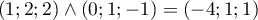 .
.
Enfin, on norme chaque vecteur: ,
,
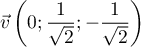 ,
et
,
et
 ,
et alors la base
,
et alors la base 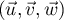 est orthonomale directe.
est orthonomale directe.
Enfin, on norme chaque vecteur: