🔍

Colles de mathématiques

Convergence d'une intégrale, IPP

Sujet

Montrer que l'intégrale I = ∫ ₁ ^+∞ ln(x)/x²dx converge et calculer sa valeur.

Corrigé de l'exercice de maths: Intégrales généralisées

Correction

La fonction 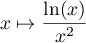$x\mapsto\dfrac{\ln(x)}{x^2}$ est continue sur 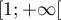$[1;+\infty[$ et l'intégrale existe sur tout segment

pour tout réel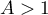

.
Il reste à étudier la convergence en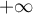 $+\infty$ . On a

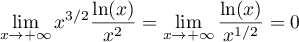
$\lim_{x\to+\infty}x^{3/2}\dfrac{\ln(x)}{x^2}=\lim_{x\to+\infty}\dfrac{\ln(x)}{x^{1/2}}=0$

par croissances comparées, ce qui montre que

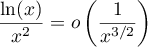
$\dfrac{\ln(x)}{x^2}=o(\dfrac1{x^{3/2}})$

et donc que l'intégrale est convergente en $+\inft$$ d'après le critère de Riemann.

Pour calculer cette intégrale, on peut penser à une intégration par parties pour enlever le logarithme en le dérivant,

$I=\int_1^{+\infty}\ln(x)\dfrac1{x^2}dx=[\ln(x)(-\dfrac1x)]_1^{+\infty}-\int_1^{+\infty}\dfrac1x(-\dfrac1x)dx=0+\int_0^{+\infty}\dfrac1{x^2}dx=[-\dfrac1x]_1^{+\infty}=1$