Colles de mathématiques
Courbe paramétrée fractions rationnelles
Sujet
Soit C la courbe définie par la représentation paramétrique
x(s)
=
11 + s2
y(s)
=
−s1 + s2
,
pour s∈[0;+∞[.
- Calculer les dérivées des fonctions x et y, puis établir le tableau des variations conjointes de x et y.
- On note A le point de la courbe lorsque s = 0,
et B le point de la courbe lorsque s = 1.
Déterminer les coordonnées des points A et B.
Préciser la direction de la tangente à la courbe C aux points A et B. - Tracer alors, en utilisant tous les résultats précédents, la courbe C.
Corrigé de l'exercice de maths: Courbes paramétrées
Correction
-
![$\la\begin{array}{ll}
x'(s)=\dfrac{-2s}{(1+s^2)^2} \\[0.3cm]
y'(s)=\dfrac{-(1+s^2)+2s^2}{(1+s^2)^2}
=\dfrac{s^2-1}{(1+s^2)^2}
\enar\right.$](/Generateur-Devoirs/Colles/courbesparam/ex4_c/1.png) d'où,
d'où,
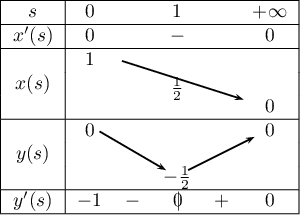
-
Lorsque
 ,
, 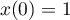 et
et 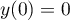 , d'où
, d'où 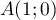 .
.
Lorsque ,
, 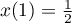 et
et 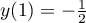 , d'où
, d'où
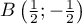 .
.
En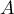 ,
, 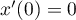 et
et 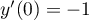 ; ainsi, la tangente en
; ainsi, la tangente en  est
verticale.
est
verticale.
En ,
, 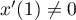 et
et 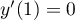 ; ainsi la tangente en
; ainsi la tangente en 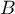 est
horizontale.
est
horizontale.
-
