Colles de mathématiques
Décomposition en série de Fourier
Sujet
Soit F la fonction créneau, 2π-périodique:
F(t) = 1
pour t∈[0, π[
F(t) = −1
pour t∈[π, 2π[
Étudier la série de Fourier de F.
Étudier la série de Fourier de F.
Corrigé de l'exercice de maths: Série de Fourier
Correction
F est 2π-périodique et impaire, et ainsi an = 0.
Par ailleurs, pour tout entier n, avec ω = 2πT = 1,
![\[b_n=\dfrac4\pi\int_0^\pi f(x)\sin(n\omega x)dx
=\dfrac4\pi\int_0\pi\sin(nx)dx
=\dfrac4\pi\Bigl[ -\dfrac1n\cos(nx)\Bigr]_0^\pi
=\dfrac{4}{n\pi}\left( 1-\cos(n\pi)\rp\]](/Generateur-Devoirs/Colles/fourier/ex0_c/6.png)
ou encore, comme ,
on obtient
,
on obtient
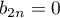 et
et  et alors
pour tout
et alors
pour tout 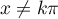 ,
, 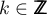 ,
,
![\[f(x)=\dfrac8\pi\sum_{n\geqslant0}\dfrac{\sin((2n+1)x)}{2n+1}\]](/Generateur-Devoirs/Colles/fourier/ex0_c/12.png)
Par ailleurs, pour tout entier n, avec ω = 2πT = 1,
ou encore, comme
![\[f(x)=\dfrac8\pi\sum_{n\geqslant0}\dfrac{\sin((2n+1)x)}{2n+1}\]](/Generateur-Devoirs/Colles/fourier/ex0_c/12.png)