🔍

Colles de mathématiques

Décomposition de Fourier d'une exponentielle périodique


Sujet


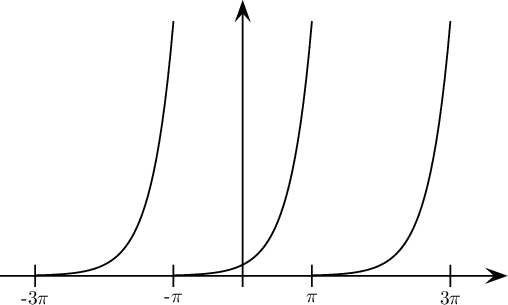
Soit f la fonction 2π-périodique telle que f (x) = ex pour x∈[−π, π[.
  1. Représenter graphiquement f sur x∈[−3π, 3π[.
  2. Déterminer la série de Fourier de f.
  3. En déduire la valeur de la somme   ∑ n≥1 1/n2 + 1

Corrigé de l'exercice de maths: Série de Fourier

Correction


f est la fonction 2π-périodique définie par l'expression f (x) = ex pour x∈[−π, π[.

  1. Courbe représentative de la fonction f


  2. La fonction est 2π-périodique donc de pulsation ω = 2π/T = 1.
    Sa valeur moyenne est
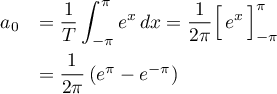
    Calcul de la valeur moyenne, le coefficient a_0


    Pour tout entier n>0, en intégrant par parties,
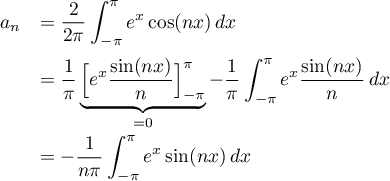
    Calcul des coefficients de Fourier a_n

    et on trouve ici l'expression des autres coefficients bn:
    \[b_n=\dfrac2{2\pi}\dsp\int_{-\pi}^\pi e^x\sin(nx)\,dx\]

    et donc, d'une part an = −1/nbn, et d'autre part, en intégrant par parties bn,
    Calcul des coefficients b_n

    Enfin, on y retrouve l'expression de an et donc, avec cos(nπ) = cos(−nπ) = (−1)n, on trouve
    \[b_n=\dfrac{(-1)^{n+1}}{n\pi}\left( e^\pi-e^{-\pi}\rp+\dfrac1na_n\]

    On a donc obtenu le système
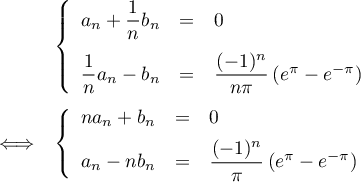
    Système reliant les coefficients a_n et b_n

    d'où on tire
    \[\la\begin{array}{ll} a_n&=\dfrac{(-1)^n\left( e^\pi-e^{-\pi}\right)}{\pi\left( n^2+1\right)}\\[1.2em] b_n&=\dfrac{(-1)^{n+1}n\left( e^\pi-e^{-\pi}\right)}{\pi\left( n^2+1\right)} \enar\right.\]


    On en déduit que pour tout réel x≠(2k + 1)π, k∈Z,
    \[f(x)=\dfrac1{2\pi}\left( e^\pi-e^{-\pi}\right) +\dfrac1\pi\left( e^\pi-e^{-\pi}\right) \sum_{n\geqslant1} \dfrac{(-1)^n\cos(nx)+(-1)^{n+1}\sin(nx)}{n^2+1}\]

  3. En x = π, on a
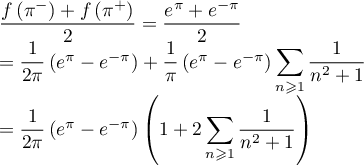
    Application du théorème de Dirichlet

    duquel on tire que
    \[\sum_{n\geqslant1} \dfrac{1}{n^2+1} =\dfrac12\lp\pi\dfrac{e^\pi+e^{-\pi}}{e^\pi-e^{-\pi}}-1\right) \]