🔍

Colles de mathématiques

Encadrement suite, intégrale et convergence série


Sujet


On considère, pour α∈R, la série de terme général un = 1 + 2 + … + n /nα
  1. Donner un encadrement de ∫ k k+1 x dx et en déduire un encadrement de vn = 1 + 2 + … + n
  2. En déduire un équivalent pour un puis la nature de la série de terme général un suivant la valeur du paramètre α .

Corrigé de l'exercice de maths: Séries - Intégrales sur un segment

Correction


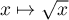  1. Comme $x\mapsto\sqrt{x}$ est croissante sur 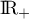$\R_+$, on a
    \[\sqrt{k}\leq\int_k^{k+1}\sqrt{x}\,dx\leq\sqrt{k+1}\]

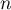    et alors, en sommant ces inégalités pour $k$ de 1 à $n$, et en utilisant la relation de Chasles pour les intégrales, on obtient
    \[v_n\leq\int_1^{n+1}\sqrt{x}\,dx\leq v_{n+1}-1\]

    L'inégalité de droite s'écrit aussi
    \[\int_1^n\sqrt{x}\,dx\leq v_n-1\]

    et on donc l'encadrement
    \[\int_1^n\sqrt{x}\,dx+1\leq v_n\leq\int_1^{n+1}\sqrt{x}\,dx\]

  2. On calcule alors les intégrales:
    \[\begin{array}{ll}\dsp\int_1^n\sqrt{x}\,dx&=\lb\dfrac23 x^{3/2}\,\rb_1^n\\[1em] &=\dfrac23\left( n^{3/2}-1\rp\enar\]

    et de même pour l'autre intégrale.
    On trouve alors que
    \[\dfrac23\left( n^{3/2}-1\rp\leq v_n\leq\dfrac23\left( (n+1)^{3/2}-1\rp\]

    et donc l'équivalent
    \[v_n\sim\dfrac23n^{3/2}\]


    On a donc
    \[u_n\sim\dfrac23n^{3/2-\alpha}=\dfrac23\,\dfrac1{n^{\alpha-3/2}}\]

    puis, par comparaison avec une série de Riemann, on en déduit que la série de terme général $u_n$ converge si et seulement si
    \[\alpha-\dfrac32>1\iff\alpha>\dfrac52\]