Colles de mathématiques
Équation de plan, projeté orthogonal et distance au plan
Sujet
Dans l'espace muni d'un repère orthonormé,
on donne trois points A(1, 2, 3), B(0, 1, 5) et C(2, 3, 4).
- Donner une équation cartésienne du plan P contenant les points A, B et C.
- Soit u, v et w trois réels, et M le point de coordonnée (u, v, w).
Déterminer le projeté orthogonal H du point M sur le plan P. - Calculer la distance du point N(2, 1, 1) au plan P.
Corrigé de l'exercice de maths: Géométrie dans l'espace
Correction
- Le produit vectoriel
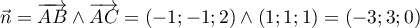 donne un vecteur normal à
donne un vecteur normal à 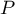 , qui a donc une équation cartésienne de
la forme
, qui a donc une équation cartésienne de
la forme  .
.
Comme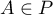 , on a
, on a 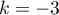 , et donc
, et donc
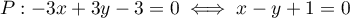 .
.
- Soit
 ,
,  .
.
On a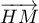 colinéaire à
colinéaire à 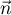 ,
donc
,
donc 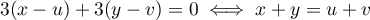 , et
, et  .
.
De plus,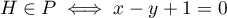 ,
d'où
,
d'où 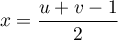 ,
, 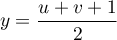 et
et  .
.
- Le projeté de
 sur
sur 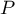 est
est 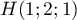 et la
la distance de
et la
la distance de 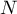 à
à  est donc
est donc