🔍

Colles de mathématiques

Étude de la convergence de la série avec un paramètre


Sujet


Soit, pour n≥1 et a > 0, la suite un = an n!/nn.
  1. Étudier la convergence de la série ∑un lorsque a≠e.
  2. Lorsque a = e, prouver que, pour n assez grand, un+1/un≥1.
    Que dire alors de la nature de la série ∑un ?

Corrigé de l'exercice de maths: Séries - Développements limités

Correction


  1. On cherche à utiliser la règle de d'Alembert et on calcule donc
    \[\begin{array}{lcl}\dfrac{u_{n+1}}{u_n}&=&\dfrac{a^{n+1}(n+1)!}{(n+1)^{n+1}}\tm\dfrac{n^n}{a^n n!}\\ &=&a\left(1+\dfrac1n\right)^{-n}\\[1.2em] &=&a\exp\Bigl(-n\ln\lp1+\frac1n\rp\Bigr)\\[1.2em] &=&a\exp\Bigl(-n\tm\lp\frac1n+o\lp\frac 1n\rp\rp\Bigr)\enar\]

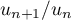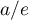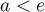    On obtient donc que $u_{n+1}/u_n$ converge vers $a/e$ et donc, d'après la règle de d'Alembert, si $a>e$, la série est divergente. Si $a<e$, la série est convergente.
    Pour $a=e$ le théorème de d'Alembert ne permet pas de conclure directement.
  2. On pousse un peu plus loin le développement précédent. On obtient
    \[\begin{array}{lcl} \dfrac{u_{n+1}}{u_n}&=&e\exp\lp-n\lp\frac1n-\frac1{2n^2}+o\lp\dfrac 1{n^2}\rp\rp\rp\\ &=&e\exp\lp-1+\dfrac{1}{2n}+o\lp\dfrac1n\rp\rp\\ &=&1+\dfrac{1}{2n}+o\lp\dfrac 1n\rp\enar\]

    En particulier, pour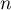 $n$ assez grand, 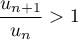$\dfrac{u_{n+1}}{u_n}>1$, et donc la suite $(u_n)$ est croissante.
    Elle ne converge donc pas vers zéro, et la série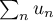 $\sum_n u_n$ est divergente.