🔍

Colles de mathématiques

Intégrale impropre avec exponentielles, et changement de variable


Sujet


On pose I = ∫ 0 +∞ e−t − e−2t/tdt.
  1. Montrer que I converge.
  2. Pour ε>0, en utilisant le changement de variable x = 2t, montrer que ∫ ε +∞ e−t − e−2t/tdt = ∫ ε 2ε e−x/xdx.
  3. Démontrer que, pour tout t≥0, 1 − t≤e−t≤1.
  4. Déduire des questions précédentes la valeur de I.
  5. En posant x = e−t, calculer ∫ 0 1 x − 1/ln(x)dx.

Corrigé de l'exercice de maths: Intégrales généralisées

Correction


  1. La fonction 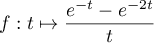$f:t\mapsto\dfrac{e^{-t}-e^{-2t}}{t}$ est continue sur $]0;+\infty[$ avec,
    \[\lim_{t\to+\infty}t^2f(t)=\lim_{t\to+\infty}t\left( e^{-t}-e^{-2t}\rp=0\]

    par croissances comparées, et donc, en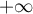 $+\infty$,
    \[f(t)=o\lp\dfrac1{t^2}\rp\]

    ce qui montre, d'après le critère de Riemann, que l'intégrale converge en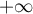 $+\infty$.

    Par ailleur, en 0, on a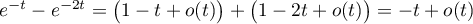 $e^{-t}-e^{-2t}=\bigl(1-t+o(t)\bigr)+\bigl(1-2t+o(t)\bigr) =-t+o(t)$ et donc
    \[\lim_{t\to0}f(t)=-1\]

    ce qui montre que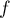 $f$ est prolongeable par continuité en 0, et en particulier que l'intégrale converge en 0.

    Finalement, on a montré que l'intégrale converge.
  2. On décompose l'intégrale, grâce à la relation de Chasles,
    \[I=\underbrace{\int_\varepsilon^{+\infty}\dfrac{e^{-t}}t\,dt}_{=I_1} -\underbrace{\int_\varepsilon^{+\infty}\dfrac{e^{-2t}}t\,dt}_{=I_2}\]

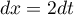    et on applique le changement de variable proposé: $x=2t$ donc $dx=2dt$ (qui est un changement de variable de class $C^1$ et strictement croissant)
    \[I_2=\int_\varepsilon^{+\infty}\dfrac{e^{-2t}}t\,dt =\int_{2\varepsilon}^{+\infty}\dfrac{e^{-x}}{\dfrac{x}2}\,\dfrac{dx}2 =\int_{2\varepsilon}^{+\infty}\dfrac{e^{-x}}{x}\,dx \]

    puis, avec à nouveau la relation de Chasles,
    \[\begin{array}{ll}I&=I_1+I_2 =\dsp\int_\varepsilon^{+\infty}\dfrac{e^{-t}}t\,dt -\int_{2\varepsilon}^{+\infty}\dfrac{e^{-x}}{x}\,dx\\[1.1em] &=\dsp\int_\varepsilon^{+\infty}\dfrac{e^{-t}}t\,dt +\int_{+\infty}^{2\varepsilon}\dfrac{e^{-x}}{x}\,dx =\int_\varepsilon^{2\varepsilon}\dfrac{e^{-x}}{x}dx \enar\]


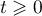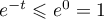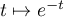  3. Pour $t\geqslant0$, on a directement que $e^{-t}\leqslant e^0=1$ par décroissance de la fonction $t\mapsto e^{-t}$.

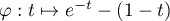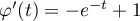    Par ailleurs, en étudiant la fonction $\varphi:t\mapsto e^{-t}-(1-t)$, on a $\varphi'(t)=-e^{-t}+1$ et donc
    \[\begin{tabular}{|c|ccccc|}\hline $t$&-$\infty$ && 0 && $+\infty$ \\\hline $\varphi'(t)$ &&$-$&0&$+$&\\\hline &&&&&\\ $\varphi$ &&\Large{$\searrow$} &&\Large{$\nearrow$} &\\ &&&0&&\\\hline \end{tabular}\]

    ce qui montre que pour tout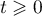 $t\geqslant0$, $\varphi(t)\geqslant0\iff e^{-t}\geqslant1-t$.
  4. D'après les questions précédentes, on a
    \[\int_\varepsilon^{2\varepsilon}\dfrac{1-x}{x}dx \leqslant \int_\varepsilon^{2\varepsilon}\dfrac{e^{-x}}{x}dx \leqslant \int_\varepsilon^{2\varepsilon}\dfrac{1}{x}dx\]


    avec, d'une part
    \[\begin{array}{ll}\dsp\int_\varepsilon^{2\varepsilon}\dfrac{1}{x}dx &=\Bigl[\ln(x)\Bigr]_\varepsilon^{2\varepsilon} =\ln(2\varepsilon)-\ln(\varepsilon)\\[1em] &=\ln\lp\dfrac{2\varepsilon}{\varepsilon}\right) =\ln(2)\enar\]

    et d'autre part,
    \[\int_\varepsilon^{2\varepsilon}\dfrac{1-x}{x}dx =\int_\varepsilon^{2\varepsilon}\dfrac1x\,dx -\int_\varepsilon^{2\varepsilon}1\,dx =\ln(2)-\varepsilon\]


    L'encadrement précédent se réécrit donc,
    \[\ln(2)-\varepsilon\leqslant \int_\varepsilon^{2\varepsilon}\dfrac{e^{-x}}{x}dx \leqslant \ln(2)\]

    puis, par le théorème des gendarmes, à la limite $\varepsilon\to0$, on obtient $I=\ln(2)$.
  5. En posant 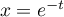$x=e^{-t}$, donc 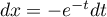$dx=-e^{-t}dt$, on a
    \[\begin{array}{ll}\dsp\int_0^1\dfrac{x-1}{\ln(x)}\,dx &=\dsp\int_{+\infty}^0\dfrac{e^{-t}-1}{-t}\lp-e^{-t}dt\rp\\[1em] &\hspace{-4em}=\dsp\int_0^{+\infty}\dfrac{e^{-t}-e^{-2t}}t\,dt =I=\ln(2)\enar\]