🔍

Colles de mathématiques

Intégrale impropre avec exponentielles, DL et changement de variable


Sujet


Soit 0≤a≤b.
  1. Justifier la convergence de ∫ 0 +∞ e−at − e−bt/tdt.
  2. Soit 0≤x≤y. Démontrer que ∫ x y e−at − e−bt/tdt = ∫ ax bx e−t/tdt − ∫ ay by e−t/tdt
  3. Démontrer que, pour tout réel z≥0, e−bz lnb/a≤ ∫ az bz e−t/tdt ≤e−az lnb/a
    En déduire que ∫ 0 +∞ e−at − e−bt/tdt = lnb/a.

Corrigé de l'exercice de maths: Intégrales généralisées

Correction


  1. Au voisinage de +∞, puisque a≥0 et b≥0, on a, par croissances comparées,
    \[\dfrac{e^{-at}-e^{-bt}}t=O\lp\dfrac1{t^2}\rp\]

    d'où la convergence de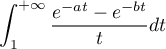 $\dsp\int_1^{+\infty}\frac{e^{-at}-e^{-bt}}tdt$ par comparaison avec une intégrale de Riemann. En 0, un développement limité montre que
    \[\dfrac{e^{-at}-e^{-bt}}t=\frac{1-at-1+bt+o(t)}{t} =\dfrac{(b-a)t+o(t)}{t}=(b-a)+o(1)\]

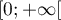    et donc que la fonction se prolonge par continuité en 0 (par sa limite $b-a$), et l'intégrale converge donc sans problème en 0. L'intégrale sur $[0;+\infty[$ converge donc bien.
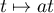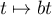  2. Avec les changements de variables $t\mapsto at$ et $t\mapsto bt$ puis par la relation de Chasles :
    \[\begin{array}{lcl} \dsp\int_x^{y}\frac{e^{-at}-e^{-bt}}{t}dt &=&\dsp\int_{ax}^{ay}\frac{e^{-t}}{t}dt-\int_{bx}^{by}\frac{e^{-t}}{t}dt\\[1.4em] &=&\dsp\int_{ax}^{bx}\frac{e^{-t}}{t}dt+\int_{bx}^{ay}\frac{e^{-t}}tdt -\int_{bx}^{ay}\frac{e^{-t}}{t}dt-\int_{ay}^{by}\frac{e^{-t}}{t}dt\\[1.4em] &=&\dsp\int_{ax}^{bx}\frac{e^{-t}}{t}dt-\int_{ay}^{by}\frac{e^{-t}}tdt \enar\]

  3. La fonction 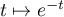$t\mapsto e^{-t}$ étant décroissante sur $\R$, on a, pour tout $t\in[az,bz]$,

    \[e^{-bz}\leq e^{-t}\leq e^{-az}\]

    puis, en multipliant par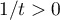 $1/t>0$ et en intégrant:
    \[\begin{array}{ll} &\dsp\int_{az}^{bz}e^{-bz}dt\leq \int_{az}^{bz}e^{-t}dt\leq \int_{az}^{bz}e^{-az}dt\\[1.5em] \iff & e^{-bz}\ln\dfrac ba \leqslant\dsp\int_{az}^{bz}\dfrac{e^{-t}}tdt \leqslant e^{-az}\ln\frac ba \enar\]

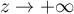  4. Il faut faire tendre, dans le résultat précédent, $z\to0$ et $z\to+\infty$.
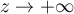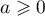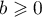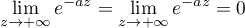    La limite lorsque $z\to0$ est, par le théorème des gendarmes, $\ln\dfrac ba$, tandis que la limite $z\to+\infty$ est nulle car $a\geqslant0$ et $b\geqslant0$ et donc $\dsp\lim_{z\to+\infty}e^{-az}=\lim_{z\to+\infty}e^{-az}=0$.
    On a vu que
    \[\int_x^{y}\frac{e^{-at}-e^{-bt}}{t}dt =\int_{ax}^{bx}\frac{e^{-t}}{t}dt-\int_{ay}^{by}\frac{e^{-t}}tdt\]

    et donc,
    \[\begin{array}{ll} \dsp\int_x^{+\infty}\frac{e^{-at}-e^{-bt}}{t}dt &=\dsp\lim_{y\to+\infty}\int_x^y\frac{e^{-at}-e^{-bt}}{t}dt\\[1.4em] &=\dsp\lim_{y\to+\infty}\lp\int_{ax}^{bx}\frac{e^{-t}}{t}dt-\int_{ay}^{by}\frac{e^{-t}}tdt\rp\\[1.4em] &=\dsp\int_{ax}^{bx}\frac{e^{-t}}{t}dt-0\enar\]

    puis,
    \[\begin{array}{ll}\dsp\int_0^{+\infty}\frac{e^{-at}-e^{-bt}}tdt &\dsp=\lim_{x\to0}\int_x^{+\infty}\frac{e^{-at}-e^{-bt}}tdt\\[1.4em] &\dsp=\lim_{x\to0}\int_{ax}^{bx}\frac{e^{-t}}{t}dt =\ln\dfrac ba\enar\]