Colles de mathématiques
Lien suite et série
Exercice de maths: Séries
Sujet
On considère une suite 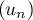 donnée par
donnée par  et
et 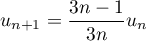 pour
pour 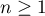 .
.
- Démontrer que
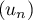 converge.
converge. - On pose, pour
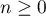 ,
, 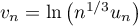 .
.
Démontrer que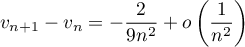 .
. - En déduire que la série de terme général
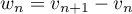 converge.
converge.
- En déduire que la suite
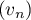 converge. On notera
converge. On notera 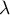 sa limite.
sa limite. - Donner un équivalent simple de
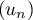 . La série de terme général
. La série de terme général 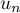 est-elle convergente ?
est-elle convergente ?