🔍

Colles de mathématiques

Limite de la dérivée d'une fonction bornée

Soit f : RR une fonction bornée et dérivable telle que lim_x+∞ f ' (x) = l .
Montrer que l = 0.

Supposons que $l\neq 0$ . On peut supposer par exemple que

.
On a donc, par définition de la limite,

$\forall\varepsilon>0, \exists A>0,\forall x\geqslant A, l-\varepsilon<f'(x)<l+\varepsilon$

En particulier, à partir d'un certain A, on a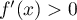

.
Par exemple en choisissant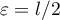 $\varepsilon=l/2$ , il existe

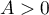tel que, pour tout $x\geq A$ , on a

$f'(x)\geq l/2$

On a alors, pour tout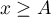 $x\geq A$ , d'après le théorème des accroissements finis,

$f(x)-f(A)=f'(c)(x-A)\geq\dfrac{l(x-A)}2$

avec $c\in[A,x]$ .
Lorsque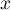

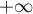vers $+\infty$ , on trouve que maintenant que

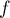tend aussi vers 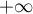$+\infty$ , ce qui est une contradictoire avec le fait qu'elle est bornée.