🔍

Colles de mathématiques

Nature de l'intégrale impropre …


Sujet


Étudier la nature de l'intégrale ∫ 0 1 ln(x) dx

Corrigé de l'exercice de maths: Intégrales généralisées

Correction


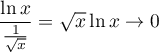x\mapsto \ln x est continue sur ]0;1]. Il suffit donc d'étudier la convergence de l'intégrale en 0. On compare pour cela à une intégrale Riemann: en 0, par croissances comparées, \dfrac{\ln x}{\frac1{\sqrt{x}}}=\sqrt{x}\ln x\to0, ce qui signifie que, en 0, \ln x=o(\dfrac1{\sqrt{x}}).
Or, x\mapsto\dfrac1{\sqrt{x}}=\dfrac1{x^{1/2}} est intégrable en 0, et donc l'intégrale est convergente.

Remarque: on peut aussi utiliser une primitive de ln(x), à savoir x ↦ xln(x)−x pour calculer l'intégrale en montrant qu'elle converge donc