Colles de mathématiques
Nature de l'intégrale impropre …
Sujet
Étudier la nature de l'intégrale
∫
0
+∞
e−x2 dx
Corrigé de l'exercice de maths: Intégrales généralisées
Correction
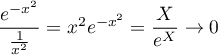 ,
ce qui signifie que, en
,
ce qui signifie que, en Or,
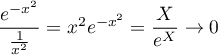 ,
ce qui signifie que, en
,
ce qui signifie que, en