Colles de mathématiques
Séries harmonique et avec coefficients binomiaux
Oral HEC - filière B/L, 2022
Exercice de maths: Séries - Annales HEC - B/L
Sujet
oral HEC, BL - 2022
Soit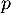 un entier naturel fixé. Pour tout entier naturel
un entier naturel fixé. Pour tout entier naturel 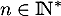 , on pose
, on pose

Soit
-
- Question de cours: rappeler les résultats de cours sur la convergence des séries de Riemann.
- Pour tout
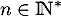 , on pose
, on pose 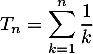 .
Montrer que
.
Montrer que
![\[\lim_{nto+\infty}T_n=+\infty\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1/6.png)
et
![\[\lim_{n\to+\infty}\dfrac{T_n}{\ln(n)}=1\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1/7.png)
- Étudier la nature de la série de terme général
 .
.
- On suppose dans toute la suite que
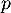 est supérieur ou égal à 2 et on pose
est supérieur ou égal à 2 et on pose
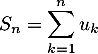 .
.
- Montrer que, pour tout entier
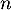 ,
,
![\[(n+p+2)u_{n+2}=(n+2)u_{n+1}\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1/12.png)
- En vous servant d'une somme télescopique, en déduire une formule pour
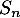 en fonction de
en fonction de 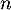 ,
,  et
et 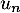 .
.
- Montrer que, pour tout entier
- Déterminer, dans les cas de convergence, la somme de la série de terme général
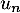 en fonction de
en fonction de 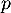 .
.