Colles de mathématiques
Séries harmonique et avec coefficients binomiaux
Oral HEC - filière B/L, 2022
Sujet
oral HEC, BL - 2022
Soit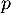 un entier naturel fixé. Pour tout entier naturel
un entier naturel fixé. Pour tout entier naturel 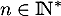 , on pose
, on pose

Soit
-
- Question de cours: rappeler les résultats de cours sur la convergence des séries de Riemann.
- Pour tout
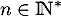 , on pose
, on pose 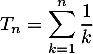 .
Montrer que
.
Montrer que
![\[\lim_{nto+\infty}T_n=+\infty\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1/6.png)
et
![\[\lim_{n\to+\infty}\dfrac{T_n}{\ln(n)}=1\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1/7.png)
- Étudier la nature de la série de terme général
 .
.
- On suppose dans toute la suite que
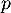 est supérieur ou égal à 2 et on pose
est supérieur ou égal à 2 et on pose
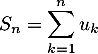 .
.
- Montrer que, pour tout entier
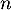 ,
,
![\[(n+p+2)u_{n+2}=(n+2)u_{n+1}\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1/12.png)
- En vous servant d'une somme télescopique, en déduire une formule pour
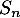 en fonction de
en fonction de 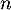 ,
,  et
et 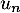 .
.
- Montrer que, pour tout entier
- Déterminer, dans les cas de convergence, la somme de la série de terme général
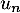 en fonction de
en fonction de 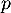 .
.
Corrigé de l'exercice de maths: Séries - Annales HEC - B/L
Correction
oral HEC, BL - 2022 - Exercice avec préparation
-
- Critère de convergence de Riemann: la série de terme général
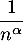 converge si et seulement si
converge si et seulement si 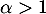
- On utilise une comparaison série/intégrale avec la fonction inverse
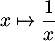 qui est strictement décroissante sur
qui est strictement décroissante sur ![$]0;+\infty[$](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/4.png) , et donc, pour tout entier
, et donc, pour tout entier 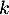 , et pour tout
, et pour tout ![$t\in[k;k+1]$](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/6.png) on a
on a
![\[\dfrac1{k+1}\leqslant\dfrac1t\leqslant\dfrac1k\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/7.png)
d'où, en intégrant terme à terme
![\[\int_k^{k+1}\dfrac{dt}{k+1}\leqslant\int_k^{k+1}\dfrac{dt}t\leqslant\int_k^{k+1}\dfrac{dt}k\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/8.png)
soit aussi en calculant ces intégrales
![\[\dfrac1{k+1}\leqslant\ln(k+1)-\ln(k)\leqslant\dfrac1k\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/9.png)
On somme ensuite terme à terme ces inégalités, de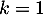 jusqu'à
jusqu'à 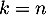 , pour faire apparaître la somme
, pour faire apparaître la somme 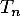
![\[T_n-1\leqslant\sum_{k=1}^n\ln(k+1)-\ln(k)\leqslant T_n\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/13.png)
et, la somme centrale étant télescopique, on trouve finalement
![\[T_n-1\leqslant \ln(n)\leqslant T_n\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/14.png)
ou encore, en retournant ces inégalités
![\[\ln(n)\leqslant T_n\leqslant \ln(n)+1\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/15.png)
D'après le théorème des gendarmes on en déduit la limite recherchée:
![\[\lim_{n\to+\infty}T_n=+\infty\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/16.png)
et, en divisant ces inégalités par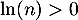 , on obtient
, on obtient
![\[1\leqslant\dfrac{T_n}{\ln(n)}\leqslant1+\dfrac1{\ln(n)}\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/18.png)
d'où la deuxième limite recherchée
![\[\lim_{n\to+\infty}\dfrac{T_n}{\ln(n)}=1\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/19.png)
ce qui signifie au passage exactement que, en ,
,
![\[T_n\sim\ln(n)\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/21.png)
- Critère de convergence de Riemann: la série de terme général
- On a
![\[\dsp\binom{n+p}{n}=\dfrac{(n+p)!}{n!\,p!}=\dfrac{(n+p)(n+p-1)\dots(n+1)}{p!}\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/22.png)
et donc (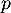 est un paramètre fixe),
est un paramètre fixe),
![\[u_n\leqslant\dfrac{p!}{n^p}\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/24.png)
et ainsi, si la série de terme général
la série de terme général  diverge, tandis qu'elle converge pour
diverge, tandis qu'elle converge pour 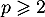 par comparaison avec une série de Riemann.
par comparaison avec une série de Riemann.
-
-
![\[\begin{array}{ll}(n+p+2)u_{n+2}&=\dfrac{n+p+2}{\binom{n+2+p}{n+2}}\\
&=\dfrac{(n+2)!p!(n+p+2)}{(n+p+2)!}\\
&=(n+2)\dfrac{(n+1)!p!}{(n+p+1)!}\\
&=(n+2)u_{n+1}
\enar\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/28.png)
- On a donc, en prenant le rang
 dans la relation précédente
dans la relation précédente
![\[(n+p)u_n=nu_{n-1}\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/30.png)
ou encore
![\[pu_n=nu_{n-1}-nu_n\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/31.png)
Pour que ce soit le terme général d'une suite télescopique, on écrit alors plutôt en retranchant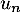 de part et d'autre
de part et d'autre
![\[(p-1)u_n=nu_{n-1}-(n+1)u_n\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/33.png)
On a alors,
![\[\sum_{k=2}^n(p-1)u_k=\dsp\sum_{k=2}^nku_{k-1}-(k+1)u_k\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/34.png)
soit
![\[\begin{array}{ll}
(p-1)\dsp\sum_{k=2}^nu_k&=\dsp\sum_{k=2}^nku_{k-1}-\sum_{k=2}^n(k+1)u_k\\
&=\dsp\sum_{k=1}^{n-1}(k+1)u_k-\sum_{k=2}^n(k+1)u_k\\
\enar\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/35.png)
ou encore
![\[(p-1)\left( S_n-u_1\right) = 2u_1-(n+1)u_n\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/36.png)
or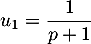 et donc
et donc
![\[S_n=-\dfrac{n+1}{p-1}u_n+\dfrac2{(p+1)(p-1)}+\dfrac1{p+1}\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/38.png)
ou encore finalement
![\[S_n=-\dfrac{n+1}{p-1}u_n+\dfrac1{p+1}\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/39.png)
-
-
On a vu que, pour
 , la série converge avec
, la série converge avec
![\[u_n\leqslant\dfrac{p!}{n^p}\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/41.png)
et donc,
![\[\begin{array}{ll}\dfrac{n+1}{p-1}u_n&\leqslant\dfrac{p!(n+1)}{(p-1)n^p}\\
&\leqslant\dfrac{p!}{p-1}\tm\dfrac{n}{n^p}\\
&=\dfrac{p!}{p-1}\tm\dfrac1{n^{p-1}}
\enar\]](/Generateur-Devoirs/Colles/Series/HEC-BL-2022-2.1_c/42.png)
qui tend vers 0 pour .
.
La somme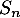 de terme général
de terme général  tend donc vers
tend donc vers 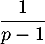 .
.