🔍

Colles de mathématiques

Simplification d'une fonction avec arctans


Sujet


Étudier la fonction f définie sur R* par f (x) = arctan x + arctan 1x .

Corrigé de l'exercice de math

Correction


On a 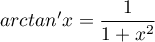$arctan'x=\dfrac{1}{1+x^2}$ et, avec 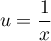$u=\dfrac1x$, $u'=-\dfrac{1}{x^2}$, $\lp\arctan u\rp'=u'\dfrac{1}{1+u^2}$, et donc
\[\begin{array}{ll} f'(x) &=\dfrac{1}{1+x^2}-\dfrac{1}{x^2}\tm\dfrac{1}{1+\dfrac{1}{x^2}}\\ &=\dfrac{1}{1+x^2}-\dfrac{1}{x^2+1}=0 \enar\]

Ainsi $f$ est constante, et, comme $f(1)=2\arctan(1)=\dfrac\pi2$, on a, pour tout $x\not=0$,
\[f(x)=\arctan x+\arctan\dfrac1x=\dfrac\pi2\]