Colles de mathématiques
Suite récurrente et série
Exercice de maths: Séries
Sujet
Soit 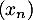 une suite de nombres réels tels que
une suite de nombres réels tels que 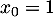 et
et 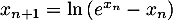 pour tout
pour tout 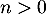 .
.
- Montrer que
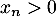 pour tout
pour tout 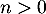 .
.
- Montrer que
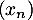 converge vers une limite qu'on déterminera.
converge vers une limite qu'on déterminera.
- Montrer que la série
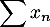 converge et calculer
la somme
converge et calculer
la somme