Colles de mathématiques
Suite récurrente et série
Sujet
Soit 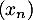 une suite de nombres réels tels que
une suite de nombres réels tels que 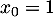 et
et 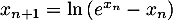 pour tout
pour tout 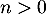 .
.
- Montrer que
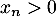 pour tout
pour tout 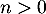 .
.
- Montrer que
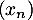 converge vers une limite qu'on déterminera.
converge vers une limite qu'on déterminera.
- Montrer que la série
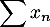 converge et calculer
la somme
converge et calculer
la somme 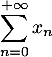
Corrigé de l'exercice de maths: Séries
Correction
D'après Ulm 2017
- On peut le montrer par récurrence.
Initialement,
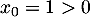 , puis, si pour un entier
, puis, si pour un entier 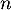 quelconque on a
quelconque on a 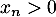 ,
alors, comme pour tout réel
,
alors, comme pour tout réel 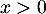 on a
on a 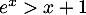 et par stricte croissance du logarithme,
et par stricte croissance du logarithme,
![\[x_{n+1}=\ln\left( e^{x_n}-x_n\right)
>\ln(1)=0\]](/Generateur-Devoirs/Colles/Series/srs_c/6.png)
ce qui montre que la propriété est héréditaire.
Ainsi, d'après le principe de récurrence, on a bien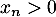 pour tout entier
pour tout entier 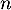 .
.
- Pour tout entier
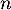 , on a
, on a
![\[\begin{array}{lcl}x_{n+1}&=&\ln\left( e^{x_n}-x_n\rp\\
&=&\ln\left( e^{x_n}\left(1-\dfrac{x_n}{e^{x_n}}\rp\rp\\[1em]
&=&\ln\left( e^{x_n}\rp+\ln\left(\left(1-\dfrac{x_n}{e^{x_n}}\rp\rp\\[1.2em]
&=&x_n+\ln\lp1-\dfrac{x_n}{e^{x_n}}\right)
\enar\]](/Generateur-Devoirs/Colles/Series/srs_c/10.png)
c'est-à-dire que
![\[x_{n+1}-x_n=\ln\lp1-\dfrac{x_n}{e^{x_n}}\rp<0\]](/Generateur-Devoirs/Colles/Series/srs_c/11.png)
car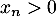 donc
donc
![\[1-\dfrac{x_n}{e^{x_n}}<1\]](/Generateur-Devoirs/Colles/Series/srs_c/13.png)
Ainsi, cette suite est décroissante.
Comme elle est de plus minorée par 0, on en conclut qu'elle converge vers une limite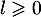 .
.
Cette limite vérifie de plus, par passage à la limite dans la relation de récurrence (ou point fixe),
![\[\begin{array}{rl}&l=\ln\left( e^l-l\rp\\
\iff&e^l=e^l-l\\
\iff&l=0\enar\]](/Generateur-Devoirs/Colles/Series/srs_c/15.png)
Cette suite converge donc vers 0. - On a, pour tout entier
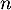 ,
,
![\[\begin{array}{rl}&x_{n+1}=\ln\left( e^{x_n}-x_n\rp\\
\iff&e^{x_{n+1}}=e^{x_n}-x_n\\
\iff&x_n=e^{x_n}-e^{x_{n+1}}\enar\]](/Generateur-Devoirs/Colles/Series/srs_c/17.png)
Ainsi, la série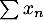 est télescopique avec, plus précisément,
est télescopique avec, plus précisément,
![\[\begin{array}{lcl}\dsp\sum_{n=0}^N x_n
&=&\dsp\sum_{n=0}^N\left( e^{x_n}-e^{x_{n+1}}\rp\\[1em]
&=&e^{x_0}-e^{x_{N+1}}\enar\]](/Generateur-Devoirs/Colles/Series/srs_c/19.png)
avec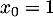 et
et
![\[\lim_{N\to+\infty}x_{N+1}=0\]](/Generateur-Devoirs/Colles/Series/srs_c/21.png)
d'où
![\[\sum_{n=0}^{+\infty}=\lim_{N\to+\infty}\sum_{n=0}^N x_n=e-1\]](/Generateur-Devoirs/Colles/Series/srs_c/22.png)