Colles de mathématiques
Sur l'espérance d'une variable aléatoire
Oral ESCP - filière B/L, 2021
Exercice de maths: Variables aléatoires discrètes - Annales ESCP - B/L
Sujet
Oral ESCP, BL - 2021
- Soit
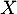 une variable aléatoire à valeurs dans
une variable aléatoire à valeurs dans 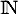 , définie sur un espace probabilisé
, définie sur un espace probabilisé 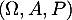 .
.
- Montrer que, pour tout
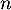 de
de 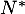 , on a:
, on a:
![\[\sum_{k=0}^nkP(X=k) = \sum_{k=0}^{n-1}P(X>k)-nP(X>n)\]](/Generateur-Devoirs/Colles/VAD/ESCP-BL-2021-4.4/6.png)
- On suppose que la série
 converge.
Démontrer que
converge.
Démontrer que  admet une espérance.
admet une espérance.
- Réciproquement, on suppose que
 admet une espérance.
admet une espérance.
Démontrer que la suite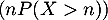 tend vers 0,
puis que la série
tend vers 0,
puis que la série 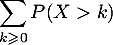 converge et enfin que
converge et enfin que
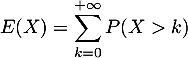
- Montrer que, pour tout
- Une application: soit
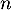 et
et 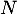 deux entiers non nuls.
On dispose d'une urne qui contient
deux entiers non nuls.
On dispose d'une urne qui contient 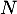 boules indiscernables au toucher numérotées de 1 à
boules indiscernables au toucher numérotées de 1 à 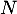 . On effectue dans cette urne,
. On effectue dans cette urne, 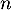 tirages successifs avec remise d'une boule et on note
tirages successifs avec remise d'une boule et on note 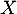 le plus grand nombre obtenu.
le plus grand nombre obtenu.
- Soit
 . Déterminer
. Déterminer 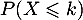 . En déduire la loi de
. En déduire la loi de  .
.
- À l'aide des questions précédentes, déterminer l'espérance de
 en fonction de
en fonction de  et
et 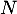 .
.
- Soit