🔍

Colles de mathématiques

Application linéaire ? Noyau et image ?


Sujet


L'application f : R2R définie par f (x, y) = x2 + y2 est-elle linéaire ?
Préciser son noyau et son image. Est-elle injective ? surjective ? bijective ?

Corrigé de l'exercice de maths: Applications linéaires

Correction


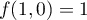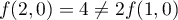f n'est clairement pas linéaire, à cause des carrés: par exemple, $f(1,0)=1$ et $f(2,0)=4\not=2f(1,0)$.

Ceci ne l'empêche pas de pouvoir être éventuellement injective, surjective, bijective.

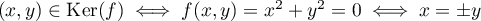$(x,y)\in\text{Ker}(f)\iff f(x,y)=x^2+y^2=0\iff x=\pm y$.
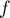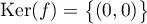Ainsi, le noyau de $f$ est réduit au vecteur nul. $\text{Ker}(f)=\bigl\{(0,0)\bigr\}$.

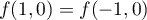Pour l'injectivité, comme f n'est pas linéaire, il faut revenir à la définition. Ici f n'est clairement pas injective car, par exemple, $f(1,0)=f(-1,0)$.

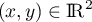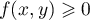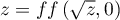f n'est pas non plus surective car, pour tout $(x,y)\in\R^2$, $f(x,y)\geqslant0$. Plus précisément, $\text{Im}(f)=\R_+$ car pour tout $z\geqslant0$ on a $z=ff\lp\sqrt{z},0\rp$.

Donc f n'est pas injective ni surjective, et donc pas non plus bijective.