🔍

Colles de mathématiques

Calcul de limite avec le théorème des accroissements finis


Sujet


Utiliser le théorème des accroissements finis, appliqué à la fonction logarithme pour démontrer que:
 limx0 ln(1 + x)x = 1

Corrigé de l'exercice de maths: Limite - Théorèmes de Rolle & accroissements finis

Correction


Soit 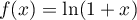$f(x)=\ln(1+x)$ continue et dérivable sur $[0;1]$. D'après le théorème des acrroissements finis sur $[0;x]$, il existe $c\in]0;x[$ tel que
\[f(x)-f(0)=(x-0)f'(c)\]

soit
\[\ln(1+x)=x\dfrac{1}{1+c}\]

ou encore
\[\dfrac{\ln(1+x)}{x}=\dfrac{1}{1+c}\]

et donc, finalement,
\[\left|\dfrac{\ln(1+x)}{x}-1\right|=\left|\dfrac{1}{1+c}-1\right|\]

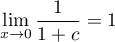Or, $c\in]0;x[$, et donc, $\dsp\lim_{x\to0}\dfrac{1}{1+c}=1$ d'où la limute recherchée:
\[\lim_{x\to0}\left|\dfrac{\ln(1+x)}{x}-1\right|=0\]

c'est-à-dire
\[\lim_{x\to0}\dfrac{\ln(1+x)}{x}=1\]