🔍

Colles de mathématiques

Calcul de limite en l'infini


Sujet


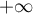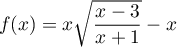
Déterminer la limite en $+\infty$ de: $f(x)=x\sqrt{\dfrac{x-3}{x+1}}-x$

Corrigé de l'exercice de maths: Développements limités

Correction


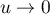Pour se ramener à 0, on pose $u=\dfrac1x\iff x=\dfrac1u$, avec donc $u\to0$ et on a alors
\[\begin{array}{ll}f(x)&=x\sqrt{\dfrac{x-3}{x+1}}-x\\[1.4em] &=\dfrac1u\sqrt{\dfrac{\frac1u-3}{\frac1u+1}}-\dfrac1u\\[1.4em] &=\dfrac1u\sqrt{\dfrac{1-3u}{1+u}}-\dfrac1u\\[1em] &=\dfrac1u\lp1-3u\rp^{1/2}\lp1+u\rp^{-1/2}-\dfrac1u \enar\]

On peut alors utiliser un développement limité:
\[\begin{array}{ll}\lp1-3u\rp^{1/2}\lp1+u\rp^{-1/2} &=\lp1-\dfrac32u+o(u)\rp\,\lp1-\dfrac12u+o(u)\rp\\[1.2em] &=1-2u+o(u) \enar\]

puis,
\[f(x)=\dfrac1u\lp1-2u+o(u)\rp-\dfrac1u =-2+o(1)\]

ce qui montre que
\[\dsp\lim_{x\to+\infty}f(x)=\lim_{u\to0}f(x)=-2\]