Colles de mathématiques
Continuité et dérivabilité d'une composée
Sujet
Soit f la fonction de R dans R
définie par
f (x) = e−1/x2
si x≠0 et
f (0) = 0.
- Montrer que pour tout k∈N, f (k)(0) = 0.
- Soit g la fonction de R dans R définie par
g(x) = f (x) si x>0 et
g(x) = 0 si x≤0.
Montrer que g est de classe C∞ sur R. - Soit a et b deux réels tels que
a<b
et soit h la fonction de R dans R définie par:
h(x) = f (x−a) si x<a 0 si x∈[a;b] f (x−b) si x>b
Montrer que h est de classe C∞ sur R.
Représenter graphiquement h pour a = 1 et b = 2.
Corrigé de l'exercice de math
Correction
- Soit
 alors
alors
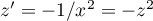 ,
et
,
et 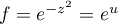 ,
et alors
,
et alors
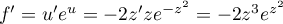 .
.
Par croissance comparée, on a bien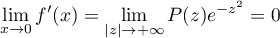 ,
et donc, en prolongeant par continuité,
,
et donc, en prolongeant par continuité,
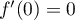 .
.
Pour démontrer le résultat général, on peut démontrer par récurrence que, pour tout entier , il existe un polynôme
, il existe un polynôme 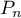 tel que
tel que
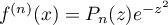 .
.
Initialement, au rang ,
, 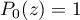 ,
et (inutile en fait ici, mais le calcul est déjà fait…)
d'après le calcul précédent,
au rang
,
et (inutile en fait ici, mais le calcul est déjà fait…)
d'après le calcul précédent,
au rang  ,
, 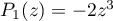 .
.
Supposons maintenant que pour un entier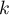 on ait
on ait 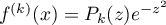 ,
alors, au rang suivant
,
alors, au rang suivant
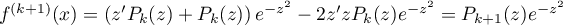 ,
,
avec le polynôme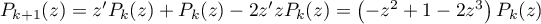 .
.
On vient ainsi de démontrer par récurrence que, pour tout entier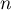 ,
il existe un polynôme
,
il existe un polynôme  tel que
tel que
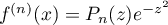 .
.
On conclut alors, avec le théorème de croissances comparées: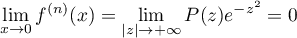 ,
et donc, en prolongeant par continuité,
,
et donc, en prolongeant par continuité,
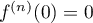 .
.
-
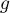 est de classe
est de classe 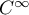 sur
sur 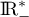 et sur
et sur  comme
composée de fonctions
comme
composée de fonctions  .
.
On a, pour tout entier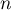 ,
,  pour tout
pour tout 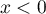 ,
et
,
et 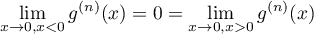 .
.
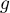 , et toutes ses dérivées succesives,
est donc dérivable à gauche et à droite en
, et toutes ses dérivées succesives,
est donc dérivable à gauche et à droite en 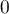 , et de dérivée continue.
, et de dérivée continue.
Ainsi,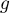 est de classe
est de classe 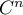 pour tout entier
pour tout entier 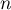 ,
c'est-à-dire
,
c'est-à-dire 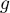 est de classe
est de classe 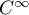 .
.
- Soit
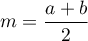 , alors sur
, alors sur  ,
on a
,
on a 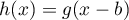 et sur
et sur ![$]-\infty;m]$](/Generateur-Devoirs/Colles/Calcul/exclcomp1_c/42.png) , on a
, on a 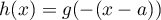 qui sont
qui sont 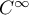 est bien
est bien 
Comme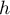 est identiquement nulle sur
est identiquement nulle sur ![$[a;b]$](/Generateur-Devoirs/Colles/Calcul/exclcomp1_c/47.png) , le raccord
entre les deux fonctions précédentes est aussi
, le raccord
entre les deux fonctions précédentes est aussi  , et donc,
, et donc,
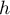 est bien
est bien 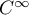 sur
sur 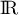 .
.
![\[\psset{xunit=1cm,yunit=4cm,arrowsize=7pt}
\begin{pspicture}(-2,-.2)(5,1)
\psline{->}(-2,0)(5,0)
\psline{->}(0,-.2)(0,1)
\psplot[linewidth=1.4pt,linecolor=blue,plotpoints=1000]{-2}{.99}{2.718 -1 x 1 sub 2 exp div exp}
\psline[linewidth=1.4pt,linecolor=blue](1,0)(2,0)
\psplot[linewidth=1.4pt,linecolor=blue,plotpoints=1000]{2.01}{5}{2.718 -1 x 2 sub 2 exp div exp}
\psline(1,-.02)(1,.02)\rput(.9,-.1){$a\!=\!1$}
\psline(2,-.02)(2,.02)\rput(2.1,-.1){$b\!=\!2$}
\end{pspicture}\]](/Generateur-Devoirs/Colles/Calcul/exclcomp1_c/52.png)