Colles de mathématiques
Courbe de Lissajous
Sujet
Étudier et tracer la courbe C d'équations paramétriques
x(t)
=
sin(2t)
y(t)
=
cos(3t)
Corrigé de l'exercice de maths: Courbes paramétrées
Correction
Les fonctions 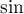 et
et 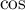 étant
étant 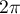 -périodiques,
on peut réduire l'intervalle d'étude dans un premier temps à
-périodiques,
on peut réduire l'intervalle d'étude dans un premier temps à ![$[-\pi,\pi]$](/Generateur-Devoirs/Colles/courbesparam/ex3_c/4.png) .
De plus, on a
.
De plus, on a 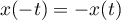 et
et  .
On peut donc encore restreindre cet intervalle à
.
On peut donc encore restreindre cet intervalle à ![$[0,\pi]$](/Generateur-Devoirs/Colles/courbesparam/ex3_c/7.png) ,
puis faire une symétrie par rapport à
,
puis faire une symétrie par rapport à 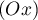 .
.
Enfin, on a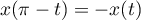 et
et 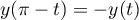 .
On peut donc encore réduire l'intervalle d'étude à
.
On peut donc encore réduire l'intervalle d'étude à ![$[0,\pi/2]$](/Generateur-Devoirs/Colles/courbesparam/ex3_c/11.png) ,
puis effectuer une symétrie par rapport à
,
puis effectuer une symétrie par rapport à 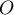 .
.
On étudie alors les variations des fonctions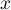 et
et 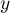 .
On a
.
On a 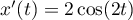 et
et 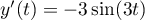 et on obtient
le tableau de variations suivant:
et on obtient
le tableau de variations suivant:
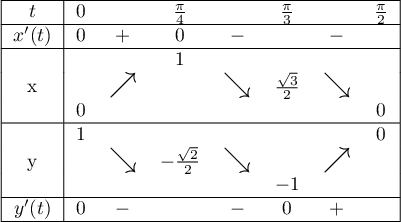
Il n'y a pas de branches infinies à étudier, et pas non plus de points stationnaires.
On a une tangente verticale au point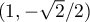 (correspondant à
(correspondant à 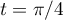 ),
et une tangente horizontale aux points
),
et une tangente horizontale aux points 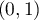 (pour
(pour  ) et en
) et en 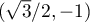 (correspondant
à
(correspondant
à 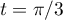 ).
On en déduit le tracé suivant
).
On en déduit le tracé suivant

Remarque:
Une courbe de Lissajous, aussi connue sous le nom de courbe de Bowditch, est la trajectoire d'un point dont les coordonnées cartésiennes ont un mouvement sinusoïdal.
Cette famille de courbes fut étudiée par Nathaniel Bowditch en 1815, puis plus en détail par Jules Lissajous en 1857.
Les courbes de Lissajous peuvent s'observer par exemple sur un oscilloscope analogique, en mode XY, dans le but notamment de mesurer un déphasage et une différence de fréquence entre deux signaux sinusoïdaux.
Enfin, on a
On étudie alors les variations des fonctions

Il n'y a pas de branches infinies à étudier, et pas non plus de points stationnaires.
On a une tangente verticale au point

Remarque:
Une courbe de Lissajous, aussi connue sous le nom de courbe de Bowditch, est la trajectoire d'un point dont les coordonnées cartésiennes ont un mouvement sinusoïdal.
Cette famille de courbes fut étudiée par Nathaniel Bowditch en 1815, puis plus en détail par Jules Lissajous en 1857.
Les courbes de Lissajous peuvent s'observer par exemple sur un oscilloscope analogique, en mode XY, dans le but notamment de mesurer un déphasage et une différence de fréquence entre deux signaux sinusoïdaux.