🔍

Colles de mathématiques

Détermination d'une limite


Sujet


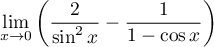
Déterminer la limite $\dsp\lim_{x\to0}\lp\dfrac2{\sin^2x}-\dfrac1{1-\cos x}\rp$

Corrigé de l'exercice de maths: Limite - Développements limités

Correction


On a 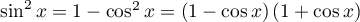$\sin^2x=1-\cos^2x=\lp1-\cos x\rp\lp1+\cos x\rp$, d'où, grâce à la décomposition en éléments simples $\dfrac{2}{(1-x)(1+x)}=\dfrac1{1-x}+\dfrac1{1+x}$,
on obtient
\[\dfrac2{1-\cos^2x}=\dfrac1{1-\cos x}+\dfrac1{1+\cos x}\]

et alors
\[\lim_{x\to0}\lp\dfrac2{\sin^2x}-\dfrac1{1-\cos x}\right) =\lim_{x\to0}\dfrac1{1+\cos x}=\dfrac12\]




On peut aussi utiliser les développements limités, si on les connaît:
\[\sin x=x-\dfrac{x^3}{6}+o\left( x^4\rp\]

et donc
\[\begin{array}{ll}\dfrac1{\sin^2 x}&=\dfrac1{\left( x-\dfrac{x^3}{6}+o\left( x^4\rp\rp^2} \\[2.6em] &=\dfrac1{x^2}\,\dfrac1{\lp1-\dfrac{x^2}{6}+o\lp x^3\rp\rp^2}\\[2.6em] &=\dfrac1{x^2}\lp1+2\dfrac{x^2}{6}+o\lp x^2\rp\rp\\[1.4em] &=\dfrac1{x^2}+\dfrac13+o(1) \enar\]

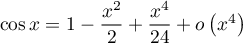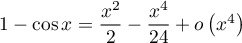et $\cos x= 1-\dfrac{x^2}2+\dfrac{x^4}{24}+o\left( x^4\rp$ donc $1-\cos x=\dfrac{x^2}2-\dfrac{x^4}{24}+o\left( x^4\rp$ et
\[\begin{array}{ll}\dfrac1{1-\cos x}&=\dfrac1{\dfrac{x^2}2}\,\dfrac1{\lp1-\dfrac{x^2}{12}+o\lp x^2\rp\rp}\\[2.6em] &=\dfrac2{x^2}\lp1+\dfrac{x^2}{12}+o\lp x^2\rp\rp\\[1.2em] &=\dfrac2{x^2}+\dfrac16+o(1)\enar\]

On obtient donc,
\[\dfrac2{\sin^2x}-\dfrac1{1-\cos x} =\dfrac23-\dfrac16+o(1)=\dfrac12+o(1)\]

d'où
\[\lim_{x\to0}\dfrac2{\sin^2x}-\dfrac1{1-\cos x}=\dfrac12\]