Colles de mathématiques
Développement en série entière d'une fonction
Sujet
Développer en série entière au voisinage de 0 la fonction
x ↦
1a − x ,
avec a≠0.
Préciser le rayon de convergence de la série entière obtenue.
Préciser le rayon de convergence de la série entière obtenue.
Corrigé de l'exercice de maths: Séries entières
Correction
On se ramène au développement en série
entière de
11 − u ,
, en factorisant par a au dénominateur:
![\[\dfrac{1}{a-x}=\dfrac{1}{a}\tm\dfrac{1}{1-\frac{x}{a}}\]](/Generateur-Devoirs/Colles/SeriesEnt/exDLSE2_c/3.png)
Pour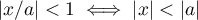 , on obtient
, on obtient
![\[\begin{array}{ll}\dfrac{1}{a-x}&\dsp=\dfrac{1}a\tm\sum_{n=0}^{+\infty}\frac{x^n}{a^n}\\[.8em]
&\dsp=\sum_{n=0}^{+\infty}\frac{x^n}{a^{n+1}}\enar\]](/Generateur-Devoirs/Colles/SeriesEnt/exDLSE2_c/5.png)
Le rayon de convergence de la série obtenue est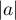 .
.
Pour
![\[\begin{array}{ll}\dfrac{1}{a-x}&\dsp=\dfrac{1}a\tm\sum_{n=0}^{+\infty}\frac{x^n}{a^n}\\[.8em]
&\dsp=\sum_{n=0}^{+\infty}\frac{x^n}{a^{n+1}}\enar\]](/Generateur-Devoirs/Colles/SeriesEnt/exDLSE2_c/5.png)
Le rayon de convergence de la série obtenue est