🔍

Colles de mathématiques

Développement en série entière d'une fonction


Sujet


Développer en série entière au voisinage de 0 la fonction x ↦ ex/1 − x. Préciser le rayon de convergence de la série entière obtenue.

Corrigé de l'exercice de maths: Séries entières

Correction


On réalise le produit de Cauchy des deux séries :
\[e^x=\sum_{n=0}^{+\infty}\frac{x^n}{n!}\]

et
\[\frac{1}{1-x}=\sum_{n=0}^{+\infty}x^n\]

La deuxième série ayant pour rayon de convergence 1, on en déduit que pour $|x|<1$, on a
\[\frac{e^x}{1-x}=\sum_{n=0}^{+\infty}a_n x^n\]

avec
\[a_n=\sum_{k=0}^n\frac{1}{k!}\]

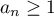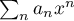La série converge pour $|x|<1$ (règle du produit de Cauchy), et comme $a_n\geq 1$, le rayon de convergence de la série obtenue est exactement égal à 1 puisque, pour $|x|>1$, la série $\sum_n a_n x^n$ diverge grossièrement puisque son terme général ne tend pas vers zéro.