🔍

Colles de mathématiques

Développement en série entière d'une fonction


Sujet


Développer en série entière au voisinage de 0 la fonction x ↦ (4 + x2)−3/2.
Préciser le rayon de convergence de la série entière obtenue.

Corrigé de l'exercice de maths: Séries entières

Correction


On factorise par 4 pour se ramener à (1+u)α. On a donc
\[(4+x^2)^{-3/2}=\frac{1}8\left(1+\frac{x^2}4\right)^{-3/2}\]

La fonction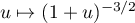 $u\mapsto (1+u)^{-3/2}$ est développable en série entière sur $]-1,1[$ et
\[\forall u\in]-1,1[,\ (1+u)^{-3/2}=1+\sum_{n\geq 1}(-1)^n\frac{3.5.7.\dots.(2n+1)}{2.4.6.\dots.2n}u^n\]

Il en résulte que pour tout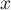 $x$ tel que $\frac{x^2}4\in]-1,1[$, on a
\[\lp1+\dfrac{x^2}4\rp^{-3/2}=1+\sum_{n\geq 1}(-1)^n\dfrac{3.5.7.\dots.(2n+1)}{2.4.6.\dots.2n}\dfrac{x^{2n}}{4^n}\]

La série entière obtenue a pour rayon de convergence $]-2,2[$.