🔍

Colles de mathématiques

Diagonalisabilité d'une matrice 2x2 symétrique réelle


Sujet


La matrice A = ab bc ∈ℳ2(R) est-elle diagonalisable ?

Corrigé de l'exercice de maths: Diagonalisation

Correction


Il s'agit d'un résultat (très) connu: toute matrice symétrique réelle est diagonalisable (d'ailleurs dans une base orthonormale de vecteurs propres).
L'objectif de l'exercice est de démontrer ce résultat dans ℳ2(R).

Méthode 1: avec le polynôme caractéristique
Le polynôme caractéristique est
\[\begin{array}{ll}\chi_A(X)=\det(A-XI)&=\left|\begin{array}{cc}a-X&b\\b&c-X\enar\right|\\[1.6em] &=(a-X)(c-X)-b^2\\[.6em] &=X^2-(a+c)X+ac-b^2\enar\]

de discriminant
\[\begin{array}{ll}\Delta&=(a+c)^2-4\left( ac-b^2\rp\\[.6em] &=a^2+c^2-2ac+4b^2\\[.6em] &=(a-c)^2+4b^2\enar\]


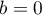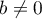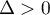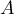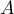Si $b=0$, la matrice est déjà diagonale. Sinon, si $b\not=0$, on a $\Delta>0$, et $A$ admet alors deux valeurs propres distinctes, et $A$ est diagonalisable.

Méthode 2: avec un calcul de rang
On calcule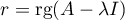 $r=\text{rg}(A-\lambda I)$, soit
\[r=\text{rg}\lp\begin{array}{cc}a-\lambda&b\\b&c-\lambda\enar\rp\]

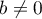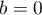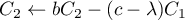
et, pour $b\not=0$ (si $b=0$, la matrice est déjà diagonale) $C_2\leftarrow bC_2-(c-\lambda)C_1$
\[r=\text{rg}\lp\begin{array}{cc}a-\lambda&b^2-(c-\lambda)(a-\lambda) \\b&0\enar\rp\]

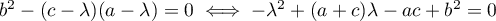Le rang est ainsi différent de 2 lorsque $b^2-(c-\lambda)(a-\lambda)=0 \iff -\lambda^2+(a+c)\lambda-ac+b^2=0$.
Le discriminant de ce trinôme est
\[\begin{array}{ll}\Delta&=(a+c)^2-4\left( ac-b^2\rp\\[.6em] &=a^2+c^2-2ac+4b^2\\[.6em] &=(a-c)^2+4b^2\enar\]

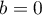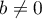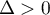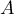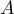Si $b=0$, la matrice est déjà diagonale. Sinon, si $b\not=0$, on a $\Delta>0$, et $A$ admet alors deux valeurs propres distinctes, et $A$ est diagonalisable.