Colles de mathématiques
Divergence de la série harmonique
Sujet
Soit la suite 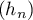 définie par
définie par
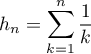 .
.
Montrer que, pour tout entier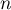 ,
, 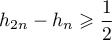 .
.
En déduire la limite de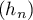 .
.
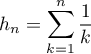 .
.
Montrer que, pour tout entier
En déduire la limite de
Corrigé de l'exercice de maths: Suites - Sommes - Limite
Correction
Pour tout  ,
,
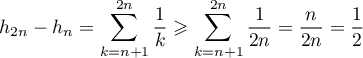 .
.
La suite est clairement strictement croissante
car
est clairement strictement croissante
car 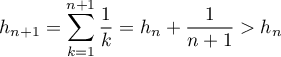 ,
et donc d'après le théorème de limite monotone,
soit
,
et donc d'après le théorème de limite monotone,
soit 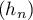 est majorée et convergente vers un réel
est majorée et convergente vers un réel 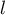 ,
soit
,
soit 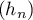 diverge vers
diverge vers 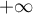 .
.
Supposons que converge vers
converge vers 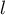 ,
alors
,
alors 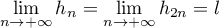 ,
et alors, comme
,
et alors, comme 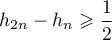 ,
on devrait avoir par passage à la limite,
,
on devrait avoir par passage à la limite,
 ,
ce qui est absurde.
,
ce qui est absurde.
Ainsi,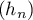 diverge vers
diverge vers 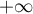 .
.
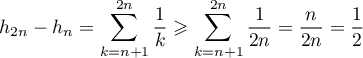 .
.
La suite
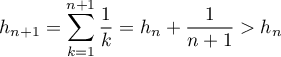 ,
et donc d'après le théorème de limite monotone,
soit
,
et donc d'après le théorème de limite monotone,
soit Supposons que
Ainsi,