Colles de mathématiques
Droites coplanaires, sécantes, …
Sujet
Soit a un réel. On considère les droites
D1
x + y = 2
y − 2z = 3
et
D2
x + y + z = 1
x − 2y + 3z = a
- D1 et D2 sont-elles parallèles ?
- Déterminer a pour qu'elles soient coplanaires.
Donner alors les coordonnées du point d'intersection de D1 et D2 et une équation du plan contenant D1 et D2.
Corrigé de l'exercice de maths: Géométrie dans l'espace
Correction
Les droites D1 et D2 sont définies par leur représentation paramétrique
D1
x + y = 2
y − 2z = 3
et
D2
x + y + z = 1
x − 2y + 3z = a
avec un paramètre a.
-
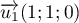 et
et 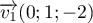 sont deux vecteurs orthogonaux
de
sont deux vecteurs orthogonaux
de 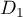 dont un vecteur directeur est donc
dont un vecteur directeur est donc
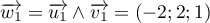 .
.
De même pour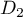 dirigée par
dirigée par
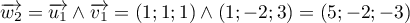 .
.
Comme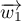 et
et 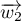 ne sont pas colinéaires,
ne sont pas colinéaires,
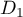 et
et  ne sont pas parallèles.
ne sont pas parallèles.
- Ces droites sont donc coplanaires si et seulement si elles
sont sécantes. Soit
 l'éventuel point d'intersection,
alors
l'éventuel point d'intersection,
alors
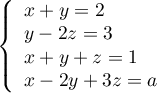 .
.
En soutrayant la 1ère équation à la 3ème, on obtient ,
et alors la 2ème fournit
,
et alors la 2ème fournit 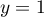 , puis la 1ère
, puis la 1ère  .
Enfin, la dernière donne alors que les droites sont sécantes
en
.
Enfin, la dernière donne alors que les droites sont sécantes
en 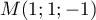 si et seulement si
si et seulement si  .
.
Un vecteur normal au plan contenant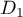 et
et 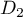 est donné par
est donné par
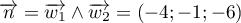 ,
donc
,
donc 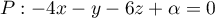 , et comme
, et comme  ,
on obtient
,
on obtient  d'où
d'où
![\[P:-4x-y-6z-1=0\iff 4x+y+6z+1=0\]](/Generateur-Devoirs/Colles/Geom3D/ex7_c/27.png)