🔍

Colles de mathématiques

Équation de droite dans le plan complexe


Sujet


Montrer que toute droite du plan a pour équation complexe: $az+\overline{az}=b$, $a\in\C^*$, $b\in\R$.

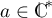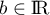Corrigé de l'exercice de maths: Nombres complexes

Correction


Soit 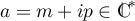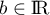$a=m+ip\in\C^*$, $b\in\R$, alors 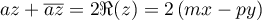$az+\overline{az}=2\Re(z)=2\left( mx-py\rp$, d'où $az+\overline{az}=b \iff mx-py=\dfrac{b}{2}$ qui est une équation de droite.
Réciproquement, soit la droite d'équation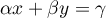 $\alpha x+\beta y=\gamma$.
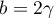D'après ce qui précède, en choisisant $a=\alpha-i\beta$ et $b=2\gamma$ on a $\alpha x+\beta y=\gamma \iff az+\overline{az}=b$.