Colles de mathématiques
Estimation de pièces défectueuses produites
Sujet
Estimation de pièces défectueuses produites
Une usine fabrique des pièces dont une proportion inconnue p est défectueuse, et on souhaite trouver une valeur approchée de p. On effectue un prélèvement de n pièces. On suppose que le prélèvement se fait sur une population très grande, et donc qu'il peut s'apparenter à une suite de n tirages indépendants avec remise. On note Xn la variable aléatoire égale au nombre de pièces défectueuses et on souhaite quantifier le fait que Xn/n approche p.
Une usine fabrique des pièces dont une proportion inconnue p est défectueuse, et on souhaite trouver une valeur approchée de p. On effectue un prélèvement de n pièces. On suppose que le prélèvement se fait sur une population très grande, et donc qu'il peut s'apparenter à une suite de n tirages indépendants avec remise. On note Xn la variable aléatoire égale au nombre de pièces défectueuses et on souhaite quantifier le fait que Xn/n approche p.
- Quelle est la loi de Xn ? Sa moyenne? Sa variance?
- Démontrer que, pour tout ε > 0, on a: P | Xnn − p|≥ε ≤14nε2
- En déduire une condition sur n pour que Xn/n soit une valeur approchée de p à 10−2 près avec une probabilité supérieure ou égale à 95%.
Corrigé de l'exercice de maths: VA: inégalités & estimation
Correction
-
 est la somme de
est la somme de 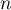 variables aléatoires de Bernoulli indépendantes de paramètre
variables aléatoires de Bernoulli indépendantes de paramètre 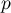 , et donc
, et donc  suit une loi binomiale
suit une loi binomiale 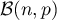 et
et
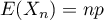 et
et  .
.
- L'inégalité de Bienaymé-Tchebychev s'écrit
![\[P(|X_n-E(X_n)|\geqslant a)\leqslant\dfrac{V(X_n)}{a^2}\]](/Generateur-Devoirs/Colles/VAIE/Estim-pieces-defectueuses_c/8.png)
Or,
![\[\left|\frac{X_n}n-p\right|\geqslant\varepsilon
\iff|X_n-np|\geqslant n\varepsilon\iff |X_n-E(X_n)|\geq n\varepsilon\]](/Generateur-Devoirs/Colles/VAIE/Estim-pieces-defectueuses_c/9.png)
On applique donc l'inégalité de Bienaymé-Tchebychev avec et on obtient
et on obtient
![\[P\Bigl(\left|\dfrac{X_n}n-p\right|\geqslant\varepsilon\Bigr)
\leqslant\dfrac {p(1-p)}{n\varepsilon^2}\]](/Generateur-Devoirs/Colles/VAIE/Estim-pieces-defectueuses_c/11.png)
De plus, sur![$[0,1]$](/Generateur-Devoirs/Colles/VAIE/Estim-pieces-defectueuses_c/12.png) , la fonction
, la fonction  admet un maximum égal
à
admet un maximum égal
à 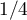 en
en 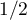 , d'où le résultat voulu.
, d'où le résultat voulu.
- On cherche
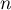 tel que
tel que
![\[P\Bigl(\left|\dfrac{X_n}n-p\right|\leqslant10^{-2}\Bigr)\geqslant0,95\]](/Generateur-Devoirs/Colles/VAIE/Estim-pieces-defectueuses_c/17.png)
soit encore, en passant à l'événement contraire
![\[P\Bigl(\left|\dfrac{X_n}n-p\right|\geqslant 10^{-2}\Bigr)\leqslant 0,05\]](/Generateur-Devoirs/Colles/VAIE/Estim-pieces-defectueuses_c/18.png)
Il suffit donc de choisir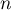 tel que
tel que
.![\[\dfrac{1}{4n10^{-4}}\leqslant0,05\iff n\geqslant 5\cdot 10^4\]](/Generateur-Devoirs/Colles/VAIE/Estim-pieces-defectueuses_c/20.png)