Colles de mathématiques
Formule des probabilités totales
Sujet
Énoncer et démontrer la formule des probabilités totales.
Corrigé de l'exercice de maths: Probabilités conditionnelles - indépendance
Correction
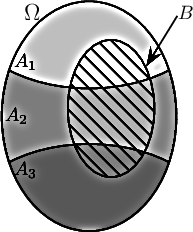
Pour trois événements, on peut représenter la situation de la façon suivante:
et
![\[P(B)=P\left( B\cap A_1\rp+P\left( B\cap A_2\rp+P\left( B\cap A_3\rp\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours2_c/2.png)
Plus généralement, pour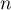 événements
événements 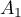 ,
, 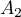 , …,
, …, 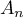 qui forment une partition de l'univers (ou un système complet),
c'est-à-dire deux à deux disjoints et dont la réunion est l'univers, on a,
pour tout événement
qui forment une partition de l'univers (ou un système complet),
c'est-à-dire deux à deux disjoints et dont la réunion est l'univers, on a,
pour tout événement 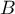 ,
,

et donc, en utilisant la définition de la probabilité conditionnelle:
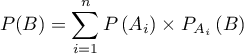
La démonstration est immédiate car
![\[B=\left( B\cap A_1\right) \cup \left( B\cap A_2\right) \cup \dots \cup \left( B\cap A_n\right)\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours2_c/10.png)
et que les événements sont deux à deux disjoints.
sont deux à deux disjoints.

et
Plus généralement, pour

et donc, en utilisant la définition de la probabilité conditionnelle:
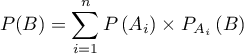
La démonstration est immédiate car
et que les événements