🔍

Colles de mathématiques

Inégalité des accroissements finis - Convergence d'une suite



Exercice de maths: Suites - Théorèmes de Rolle & accroissements finis

Sujet


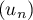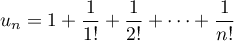On considère la suite $\left( u_n\rp$ définie par $u_n=1+\dfrac{1}{1!}+\dfrac{1}{2!}+\dots+\dfrac{1}{n!}$.
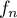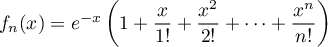Pour tout entier $n$, on définit de plus la fonction $f_n$ définie par $f_n(x)=e^{-x}\lp1+\dfrac{x}{1!}+\dfrac{x^2}{2!}+\dots+\dfrac{x^n}{n!}\rp$.

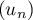En utilisant l'inégalité des accroissements finis appliquée à $f_n$ sur $[0;1]$ montrer la suite $\left( u_n\rp$ converge, et déterminer sa limite.

Correction