🔍

Colles de mathématiques

Matrice redondante diagonalisable ?


Sujet


On considère la matrice
A = 111 111 111
  1. A est-elle diagonalisable ? Si oui, donner une base de vecteurs propres de A.
  2. A est-elle inversible ?
  3. A est-elle une projection ?

Corrigé de l'exercice de maths: Diagonalisation

Correction


  1. A est une matrice symétrique réelle: A est donc diagonalisable (théorème spectral).

    On peut aussi (et doit savoir) détailler les calculs du spectre et de la dimension des espaces propres, (ce qu'il faut de toute façon faire pour donner une base de vecteurs propres). Le polynôme caractéristique de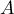 $A$ est
    \[\chi_A(x)=\det\left( xI_3-A\right) =\left|\begin{array}{ccc}x-1&-1&-1\\-1&x-1&-1\\-1&-1&x-1\enar\right|\]


    En additionnat toutes les colonnes, $C_1\leftarrow C_1+C_2+C_3$, on obtient
    \[\chi_A(x)=\left|\begin{array}{ccc}x-3&-1&-1\\x-3&x-1&-1\\x-3&-1&x-1\enar\right| =(x-3)\left|\begin{array}{ccc}1&-1&-1\\1&x-1&-1\\1&-1&x-1\enar\right|\]

    puis en soustrayant la ligne 1 à la deuxième et à la troisième, $L_2\leftarrow L_2-L_1$ et $L_3\leftarrow L_3-L_1$,
    \[\chi_A(x)=(x-3)\left|\begin{array}{ccc}1&-1&-1\\0&x&0\\0&0&x\enar\right| =(x-3)x^2\]

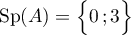    Ainsi, le spectre de $A$ est $\text{Sp}(A)=\Bigl\{ 0 \, ; 3 \Bigr\}$.
    L'espace propre associé à la valeur propre 3 est nécessairement de dimension 1. Soit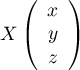 $X\lp\begin{array}{c}x\\y\\z\enar\rp$ alors
    \[AX=3X\iff\la\begin{array}{ll}-2x+y+z=0\\x-2y+z=0\\x+y-2z=0\enar\right.\]

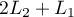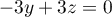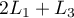    En effectuant $2L_2+L_1$, on obtient $-3y+3z=0$ soit $y=z$, et de même $2L_1+L_3$ donne $-3x+3y=0$ soit $x=y$.
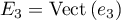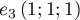    Finalement, l'espace propre associé à la valeur propre 3 est $E_3=\text{Vect}\left( e_3\rp$ avec $e_3\left(1;1;1\rp$.

    Il reste à préciser le noyau, espace propre associé à la valeur propre nulle.
    Soit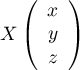 $X\lp\begin{array}{c}x\\y\\z\enar\rp$ alors
    \[AX=0\iff\la\begin{array}{ll}x+y+z=0\\x+y+z=0\\x+y+z=0\enar\right.\]

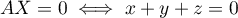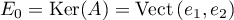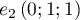    Ainsi, $AX=0\iff x+y+z=0$ qui est une équation de plan, donc de dimension 2, tout comme la multiplicité de la valeur propre nulle. L'espace propre associé à la valeur propre nulle est $E_0=\text{Ker}(A)=\text{Vect}\left( e_1,e_2\rp$ avec $e_1\left(1;1;0\rp$ et $e_2\left(0;1;1\rp$.

    A est ainsi diagonalisable dans la base de vecteurs propres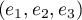 $\left( e_1,e_2,e_3\rp$.
  2. Les calculs précédents montrent que le noyau de A n'est pas réduit au vecteur nul: A n'est pas inversible.
  3. Comme 3 est valeur propre, A ne peut pas être un projecteur (pour lequel les seules valeurs propres possibles sont 0 et 1).
    On peut aussi calculer A2 et trouver que A2 = 3A, donc A n'est pas un projecteur.