Colles de mathématiques
Matrices orthogonales, antisymétriques et valeurs propres
Oral HEC - filière B/L, 2022
Exercice de maths: Diagonalisation - Annales HEC - B/L
Sujet
oral HEC, BL - 2022 - Sujet avec préparation
Soit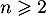 un entier.
Si
un entier.
Si 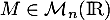 est une matrice, on note
est une matrice, on note  sa transposée.
sa transposée.
On dit qu'une matrice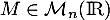 est orthogonale si
est orthogonale si 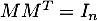 .
.
On dit qu'une matrice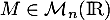 est symétrique si
est symétrique si 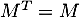 .
.
On dit qu'une matrice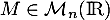 est antisymétrique si
est antisymétrique si  .
.
On confond dans la suite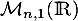 avec
avec 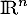 que l'on munit de son produit scalaire canonique noté
que l'on munit de son produit scalaire canonique noté 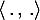 et de la norme associée notée
et de la norme associée notée  .
.
Soit
On dit qu'une matrice
On dit qu'une matrice
On dit qu'une matrice
On confond dans la suite
- Question de cours : rappeler la définition d'une matrice inversible.
-
- Montrer que toute matrice orthogonale est inversible.
- Soit
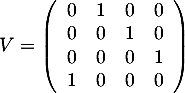 .
Préciser pour quelle(s) valeur(s) de
.
Préciser pour quelle(s) valeur(s) de 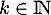 , la matrice
, la matrice 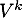 est orthogonale.
est orthogonale.
- Soit
 une matrice antisymétrique de
une matrice antisymétrique de 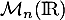 .
Soit
.
Soit 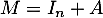 et
et 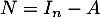 .
.
- Soit
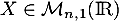 . Calculer
. Calculer 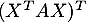 et en déduire la valeur de
et en déduire la valeur de 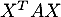 .
.
- Montrer que la seule valeur propre possible pour
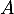 est 0.
Dans quel cas la matrice
est 0.
Dans quel cas la matrice 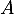 est-elle diagonalisable ?
est-elle diagonalisable ?
- Montrer que les matrices
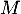 et
et 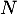 sont inversibles.
sont inversibles.
- Montrer que les matrices
 et
et 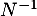 commutent.
commutent.
- Montrer que la matrice
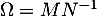 est orthogonale.
est orthogonale.
-
 est-il valeur propre de
est-il valeur propre de 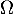 ?
?
- Soit
- Soit
 une matrice orthogonale de
une matrice orthogonale de 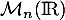 n'admettant pas
n'admettant pas 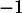 comme valeur propre. Montrer qu'il existe une unique matrice antisymétrique
comme valeur propre. Montrer qu'il existe une unique matrice antisymétrique 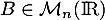 telle que
telle que
![\[U=(I_n+B)(I_n-B)^{-1}\]](/Generateur-Devoirs/Colles/Diagonalisation/HEC-BL-2022-1.1/37.png)